
37.已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,
D、F分别为AC、PC的中点,DE⊥AP于E.
(1)求证:AP⊥平面BDE;
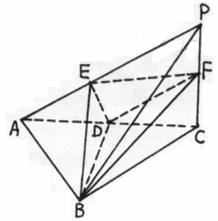
(2)求证:平面BDE⊥平面BDF;
(3)若AE∶EP=1∶2,求截面BEF分三棱锥
P-ABC所成两部分的体积比.
36.(’85广东)已知直三棱柱ABC-A1B1C1的侧棱AA1=4cm,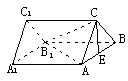
它的底面△ABC中有AC=BC=2cm,∠C=90o,E是AB的
中点.
(1) 求证:CE和AB1所在的异面直线的距离等于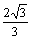 cm;
cm;
(2) 求截面ACB1与侧面ABB1A1所成的二面角的大小.
35. 如图1,直角梯形ABCD中,∠BAD=∠D=90o,AD=CD=a,AB=2a,
将△ADC沿AC折起,使点D到DM.
(1) 若二面角DM-AC-B为直二面角(图2),求二面角DM-BC-A的大小;
(2) 若二面角DM-AC-B为60o(图3),求三棱锥DM-ABC的体积.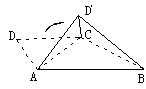




图1 图2 图3
34. 已知直三棱柱ABC-A1B1C1中,AB=AC,F为BB1上的一点,BF=BC=2a,
FB1=a.
(1) 若D为BC的中点,E为AD上不同于A、D的任一点,求证:EF⊥FC1;
(2) 若A1B1=3a,求FC1与平面AA1B1B所成角的大小.
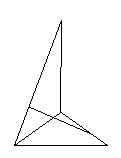
33. 如图,平面a∩平面b=MN,
二面角A-MN-B为60o,点A∈a,
B∈b,C∈MN,∠ACM=∠BCN=45o.
AC=1, 
(1) 求点A到平面b的距离;
(2) 求二面角A-BC-M的大小. 第33题图
32. 直二面角
直二面角 中,
中,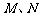 分别是线段
分别是线段 上的点(不包括端点),
上的点(不包括端点),
且 ,
,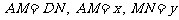 。
。
(1)若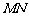 与平面
与平面 所成的角为
所成的角为 ,求
,求 的值;
的值;
(2)求函数 的解析式及定义域、值域。
的解析式及定义域、值域。
31.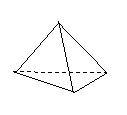 三棱锥
三棱锥 中,
中, ,其余棱长均为1。
,其余棱长均为1。
(1)求证: ;
;
(2)求三棱锥 的体积的最大值。
的体积的最大值。
30.设 是空间的不同直线或不同平面,且直线不在平面内,下列条件中能保证“若
是空间的不同直线或不同平面,且直线不在平面内,下列条件中能保证“若
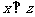 ,且
,且 ”为真命题的是
(填所有正确条件的代号)
”为真命题的是
(填所有正确条件的代号)
①x为直线,y,z为平面 ②x,y,z为平面
③x,y为直线,z为平面 ④x,y为平面,z为直线
⑤x,y,z为直线
29.α,β是两个不同的平面,m , n 是平面α及β之外的两条不同直线,给出四个论断:
①m⊥n; ②α⊥β;③n⊥β; ④m⊥α,以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题 .
28.正三棱锥S-ABC的侧棱长为1,两条侧棱的夹角为45°,过顶点A作一截面交SB于D,交SC于E,则△ADE的周长的最长小值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com