
1.1
二次函数的一般式
 中有三个参数
中有三个参数 . 解题的关键在于:通过三个独立条件“确定”这三个参数.
. 解题的关键在于:通过三个独立条件“确定”这三个参数.
例1 已知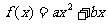 ,满足1
,满足1 且
且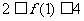 ,求
,求 的取值范围.
的取值范围.
分析:本题中,所给条件并不足以确定参数 的值,但应该注意到:所要求的结论不是
的值,但应该注意到:所要求的结论不是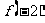 的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1
的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1 和
和 当成两个独立条件,先用
当成两个独立条件,先用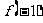 和
和 来表示
来表示 .
.
解:由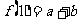 ,
, 可解得:
可解得:
 (*)
(*)
将以上二式代入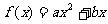 ,并整理得
,并整理得
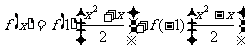 ,
,
∴ 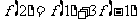 .
.
又∵
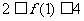 ,
, ,
,
∴  .
.
例2 设 ,若
,若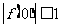 ,
,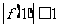 ,
, , 试证明:对于任意
, 试证明:对于任意 ,有
,有 .
.
分析:同上题,可以用 来表示
来表示 .
.
解:∵  ,
,
∴  ,
,
∴  .
.
∴ 当 时,
时,

当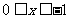 时,
时,


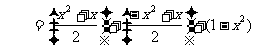
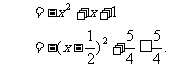
综上,问题获证.
1. 代数推理
由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质.
28.(本小题12分)九(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
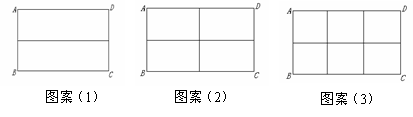
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为 m,长方形框架ABCD的面积为S=
(用含
m,长方形框架ABCD的面积为S=
(用含 的代数式表示);当AB=
m时, 长方形框架ABCD的面积S最大;
的代数式表示);当AB=
m时, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为 m,设AB为
m,设AB为 m,当AB=________m时,长方形框架ABCD的面积S最大.
m,当AB=________m时,长方形框架ABCD的面积S最大.
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律.
探索:如图案(4),
 如果铝合金材料总长度为
如果铝合金材料总长度为 m共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.
m共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.
26.(本小题10分)已知:抛物线C1: 与C2:
与C2: 具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
(1)求m,n的值;
(2)试写出x为何值时,y1 >y2?
(3)试描述抛物线C1通过怎样的变换得到抛物线C2.
27(本小题12分)如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数)
(1)求点P6的坐标;
(2)求△P5OP6的面积;
(3)我们规定:把点Pn(xn,yn)(n=10,1,2,3,…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,| yn|)称之为点Pn的“绝对坐标”.根据图中点Pn的分布规律,请你猜想点Pn的“绝对坐标”,并写出来.

25.(本小题10分)有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
(1)求被剪掉阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

24.(本小题10分)元旦前夕,我市为美化市容,开展城市绿化活动,要种植一种新品种树苗.甲、乙两处育苗基地均以每株4元的价格出售这种树苗,并对一次性购买该种树苗不低于1000株的用户均实行优惠:甲处的优惠政策是每株树苗按原价的7.5折出售;乙处的优惠政策是免收所购树苗中200株的费用,其余树苗按原价的9折出售.
(1)规定购买该种树苗只能在甲、乙两处中的一处购买,设一次性购买x(x≥1000且x为整数)株该种树苗,若在甲处育苗基地购买,所花的费用为y1元,写出y1与x之间的函数关系式,若在乙处育苗基地购买,所花的费用为y2元,写出y2与x之间的函数关系式(两个关系式均不要求写出自变量x的取值范围);
(2)若在甲、乙两处分别一次性购买1400株该种树苗,在哪一处购买所花的费用少?为什么?
(3)若在甲育苗基地以相应的优惠方式购买一批该种树苗,又在乙育苗基地以相应的优惠方式购买另一批该种树,两批树苗共2500株,购买2500株该树苗所花的费用至少需要多少元?这时应在甲、乙两处分别购买该种树苗多少株?
23.(本小题10分)如图1,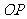 是
是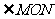 的平分线,请你在该图形上利用尺规作出一对以
的平分线,请你在该图形上利用尺规作出一对以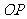 所在直线为对称轴的全等三角形.
所在直线为对称轴的全等三角形.
请你参考这个作全等三角形的方法,解答下列问题:
如图2,在 中,
中,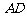 ,
, 分别是
分别是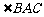 ,
, 的平分线,且
的平分线,且 =
=
 证明:
证明: .
.
22.(本小题8分)小华与小丽设计了A,B两种游戏:
游戏A的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
游戏B的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
(1)请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
(2)若游戏A和B对于两人都不公平,则请你修改游戏A或游戏B,使修改后的规则,对于两人都公平.
21.(本小题8分)为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.
|
|||
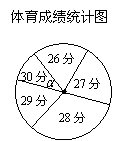 |
|||
|
体育成绩(分) |
人数(人) |
百分比(%) |
|
26 |
8 |
16 |
|
27 |
|
24 |
|
28 |
15 |
|
|
29 |
m |
|
|
30 |
|
|
根据上面提供的信息,回答下列问题:
(1)写出样本容量,m的值及抽取部分学生体育成绩的中位数;
(2)已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
20.(本小题8分)如图,小强在江南岸选定建筑物A,并在江北岸的B处观察,此时,视线与江岸BE所成的夹角是30°,小强沿江岸BE向东走了500m,到C处,再观察A,此时视线AC与江岸所成的夹角∠ACE=60°.根据小强提供的信息,你能测出江宽吗?若能,写出求解过程(结果可保留根号);若不能,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com