
1.什么叫从集合到集合上的映射?
4.分别令x=0,y=0得两个焦点F1(0,-3),F2(4,0),从而可得抛物线方程为x2=-12y或y2=16x
3.(1)y2=24x,y2=-2x
(2)x2=-12y(图略)
4.求焦点在直线3x-4y-12=0上的抛物线的标准方程.
作业答案:


3.根据下列条件,求抛物线的方程,并描点画出图形:
(1)顶点在原点,对称轴是x轴,并且顶点与焦点的距离等于6;
(2)顶点在原点,对称轴是y轴,并经过点p(-6,-3).

到准线的距离是多少?点M的横坐标是多少?
2.求下列抛物线的焦点坐标和准线方程:
(1)x2=2y;(2)4x2+3y=0;
(3)2y2+5x=0;(4)y2-6x=0.
(五)小结
本次课主要介绍了抛物线的定义,推导出抛物线的四种标准方程形式,并加以运用.
(四)四种标准方程的应用
例题:(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.


方程是x2=-8y.
练习:根据下列所给条件,写出抛物线的标准方程:
(1)焦点是F(3,0);

(3)焦点到准线的距离是2.
由三名学生演板,教师予以订正.答案是:(1)y2=12x;(2)y2=-x;(3)y2=4x,y2=-4x,x2=4y,x2=-4y.
这时,教师小结一下:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程.当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解.
(三)抛物线的标准方程
设定点F到定直线l的距离为p(p为已知数且大于0).下面,我们来求抛物线的方程.怎样选择直角坐标系,才能使所得的方程取较简单的形式呢?
让学生议论一下,教师巡视,启发辅导,最后简单小结建立直角坐标系的几种方案:
方案1:(由第一组同学完成,请一优等生演板.)
以l为y轴,过点F与直线l垂直的直线为x轴建立直角坐标系(图2-
30).设定点F(p,0),动点M的坐标为(x,y),过M作MD⊥y轴于D,抛物线的集合为:p={M||MF|=|MD|}.

化简后得:y2=2px-p2(p>0).
方案2:(由第二组同学完成,请一优等生演板)

以定点F为原点,平行l的直线为y轴建立直角坐标系(图2-31).设动点M的坐标为(x,y),且设直线l的方程为x=-p,定点F(0,0),过M作MD⊥l于D,抛物线的集合为:
p={M||MF|=|MD|}.

化简得:y2=2px+p2(p>0).
方案3:(由第三、四组同学完成,请一优等生演板.)

取过焦点F且垂直于准线l的直线为x轴,x轴与l交于K,以线段KF的垂直平分线为y轴,建立直角坐标系(图2-32).
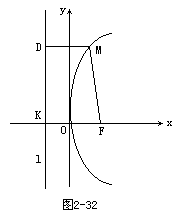

抛物线上的点M(x,y)到l的距离为d,抛物线是集合p={M||MF|=d}.

化简后得:y2=2px(p>0).
比较所得的各个方程,应该选择哪些方程作为抛物线的标准方程呢?
引导学生分析出:方案3中得出的方程作为抛物线的标准方程.这是因为这个方程不仅具有较简的形式,而方程中的系数有明确的几何意义:一次项系数是焦点到准线距离的2倍.
由于焦点和准线在坐标系下的不同分布情况,抛物线的标准方程有四种情形(列表如下):
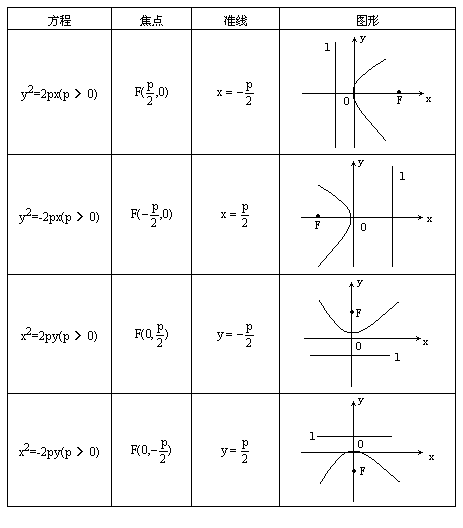
将上表画在小黑板上,讲解时出示小黑板,并讲清为什么会出现四种不同的情形,四种情形中P>0;并指出图形的位置特征和方程的形式应结合起来记忆.即:当对称轴为x轴时,方程等号右端为±2px,相应地左端为y2;当对称轴为y轴时,方程等号的右端为±2py,相应地左端为x2.同时注意:当焦点在正半轴上时,取正号;当焦点在负半轴上时,取负号.
(二)抛物线的定义
1.回顾
平面内与一个定点F的距离和一条定直线l的距离的比是常数e的轨迹,当0<e<1时是椭圆,当e>1时是双曲线,那么当e=1时,它又是什么曲线?
2.简单实验
如图2-29,把一根直尺固定在画图板内直线l的位置上,一块三角板的一条直角边紧靠直尺的边缘;把一条绳子的一端固定于三角板另一条直角边上的点A,截取绳子的长等于A到直线l的距离AC,并且把绳子另一端固定在图板上的一点F;用一支铅笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺左右滑动,这样铅笔就描出一条曲线,这条曲线叫做抛物线.反复演示后,请同学们来归纳抛物线的定义,教师总结.

3.定义
这样,可以把抛物线的定义概括成:
平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上).定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com