(一)、复习提问：

　　　 　1、交集并集的概念，

　　　 2、交集和并集的符号表示

重点：补集的概念

1理解在给定集合中，一个子集的补集的含义，会求给定子集的补集 .

2. 能使用Venn图表达集合的关系及运算，体会直观图示对理解抽象概念的作用 .

2、课本P11　 4

作业

课本P12　 A组9、10

2、交集和并集的符号表示

1、交集并集的概念，

(四)．作业P 12习题1.1A组第6、7题

(三)．归纳小结：

通过本节课的学习,要正确理解交集、并集的概念，这是进行集合间的交、并运算的关键。理解概念时要注意从文字语言、符号语言、图形语言三个方面来理解。注意利用图、数轴来解决问题，充分体现数形结合的思想。

(二)、新课讲解

　 l.并集

　　 -般地，由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集.

　　 记作：A∪B.　　 　读作：A并B.

　　 其含义用符号表示为：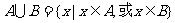

用Venn图表示：

请同学们用并集运算符号表示问题1中A，B，C三者之间的关系.

例5： (1)设A={4，5，6，8)，B={3，5，7，8)，求A∪B.

　　　　　 (2设集合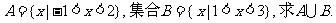

学生独立完成后强调：

　 (1)在求两个集合的并集时，它们的公共元素在并集中只能出现一次.

　　 (2)对于表示不等式解集的集合的运算，可借助数轴解题.

　2.交集

　 (1)思考：求集合的并集是集合间的一种运算，那么集合间还有其他运算吗？

请同学们考察下面的问题，集合A.B与集合C之间有什么关系？

①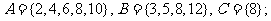

②B={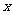|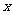是汽车三中2009年9月在校的高一年级同学}，C={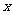|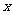是汽车三中2009年9月在校的高一年级女同学}.

组织学生思考，讨论和交流，得出结论，从而得出交集的定义；

一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集.

记作：A∩B.读作：A交B

其含义用符号表示为：

接着要求学生用Venn图表示交集运算.

例题6：

学校里开运动会，设A={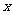|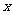是参加一百米跑的同学}，B={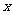|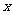是参加二百米跑的同学}，C={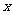|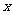是参加四百米跑的同学}，集合运算A∩B与A∩C的含义.

例7：设平面内直线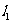上点的集合为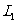，直线上点的集合为，试用集合的运算表示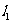_，的位置关系。

学生独立练习，教师检查，作个别指导.并对学生中存在的问题进行反馈和纠正.