3．几个重要的三角变换：

sin α cos α可凑倍角公式；　 1±cos α可用升次公式；

1±sin α 可化为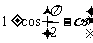，再用升次公式；

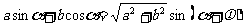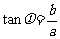(其中 )这一公式应用广泛，熟练掌握．

2．三角变换的一般思维与常用方法．

注意角的关系的研究，既注意到和、差、倍、半的相对性，如 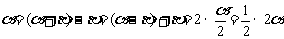．也要注意题目中所给的各角之间的关系．

注意函数关系，尽量异名化同名、异角化同角，如切割化弦，互余互化，常数代换等．

熟悉常数“1”的各种三角代换：

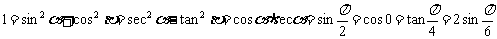等．

注意万能公式的利弊：它可将各三角函数都化为的代数式，把三角式转化为代数式．但往往代数运算比较繁．

熟悉公式的各种变形及公式的范围，如

　sin α = tan α · cos α 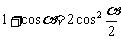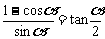，，等．

利用倍角公式或半角公式，可对三角式中某些项进行升降幂处理，如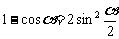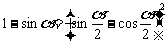，，等．从右到左为升幂，这种变形有利用根式的化简或通分、约分；从左到右是降幂，有利于加、减运算或积和(差)互化．

对于三角函数进行恒等变形，是三角知识的综合应用，其题目类型多样，变化似乎复杂，处理这类问题，注意以下几个方面：

1．三角函数式化简的目标：项数尽可能少，三角函数名称尽可能少，角尽可能小和少，次数尽可能低，分母尽可能不含三角式，尽可能不带根号，能求出值的求出值．

4.解答三角高考题的策略。

(1)发现差异：观察角、函数运算间的差异，即进行所谓的“差异分析”。

(2)寻找联系：运用相关公式，找出差异之间的内在联系。

(3)合理转化：选择恰当的公式，促使差异的转化。

3.证明三角不等式的方法：比较法、配方法、反证法、分析法，利用函数的单调性，利用正、余弦函数的有界性，利用单位圆三角函数线及判别法等。

2.证明三角等式的思路和方法。

(1)思路：利用三角公式进行化名，化角，改变运算结构，使等式两边化为同一形式。

(2)证明方法：综合法、分析法、比较法、代换法、相消法、数学归纳法。

1.三角函数恒等变形的基本策略。

(1)常值代换：特别是用“1”的代换，如1=cos²θ+sin²θ=tanx·cotx=tan45°等。

(2)项的分拆与角的配凑。如分拆项：sin²x+2cos²x=(sin²x+cos²x)+cos²x=1+cos²x；配凑角：α=(α+β)－β，β=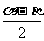－等。

(3)降次与升次。即倍角公式降次与半角公式升次。

(4)化弦(切)法。将三角函数利用同角三角函数基本关系化成弦(切)。

(5)引入辅助角。asinθ+bcosθ=sin(θ+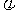)，这里辅助角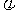所在象限由a、b的符号确定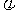，角的值由tan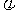=确定。

(6)万能代换法。巧用万能公式可将三角函数化成tan的有理式。

(二)三角函数性质的分析

1．三角函数的定义域

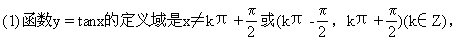
这两种表示法都需要掌握．即角x不能取终边在y轴上的角．

函数y=cotx的定义域是x≠π或(kπ，kπ+π)(k∈Z)，这两种表示法都需要掌握．即角x不能取终边在x轴上的角．

(2)函数y=secx、y=cscx的定义域分别与y=tanx、y=cotx相同．

2．三角函数的值域

(1)由|sinx|≤1、|cosx|≤1得函数y=cscx、y=secx的值域是|cscx|≥1、|secx|≥1．

(2)复合三角函数的值域问题较复杂，除了代数求值域的方法都可以适用外，还要注意三角函数本身的特点，特别是经常需要先进行三角变换再求值域．

常用的一些函数的值域要熟记．

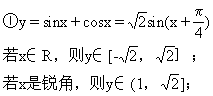
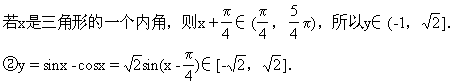
③y=tanx+cotx∈(-∞，-2]∪[2，+∞)．

3．三角函数的周期性

(1)对周期函数的定义，要抓住两个要点：

①周期性是函数的整体性质，因此f(x+T)=f(x)必须对定义域中任一个x成立时，非零常数T才是f(x)的周期．

②周期是使函数值重复出现的自变量x的增加值．

因为sin(2kπ+x)=sinx对定义域中任一个x成立，所以2kπ(k∈Z，k≠0)是y=sinx的周期，最小正周期是2π．

同理2kπ(k∈Z，k≠0)是y=cosx的周期，最小正周期是2π．

因为tan(kπ+x)=tanx对定义域中任一个x成立，所以kπ(k∈Z，k≠0)是y=tanx的周期，最小正周期是π．

同理kπ(k∈Z，k≠0)是y=cotx的周期，最小正周期是π．

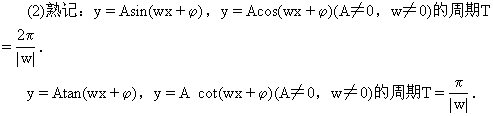
(3)三角函数的周期性在三角函数性质中的作用

①函数的递增或递减区间周期性的出现，每一个三角函数，都有无数个递增或递减区间，这些递增区间互不连接，递减区间也互不连接．

②函数的最大、最小值点或使函数无意义的点周期性变化．

③因为三角函数是周期函数，所以画三角函数图象时，只须画一个周期的图象即可．

4．三角函数的奇偶性，单调性

研究函数的单调性，关键是求函数的单调区间．

5．三角函数的图象

(1)画三角函数的图象应先求函数的周期，然后用五点法画出函数一个周期的图象．

(2)函数y=sinx，y=cosx，y=tanx，y=cotx　 图象的对称中心分别为

∈Z)的直线．

(一)三角变换公式的使用特点

1．同角三角函数关系式

(1)理解公式中“同角”的含义．

(2)明确公式成立的条件。

例如，tan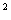α+1=sec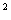α，当且仅当≠k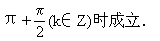

(3)掌握公式的变形．特别需要指出的是 sinα=tanα·cosα，

cosα=cotα·sinα．它使得“弦”可以用“切”来表示．

(4)使用这组公式进行变形时，经常把“切”、“割”用“弦”表示，即化弦法，这是三角变换非常重要的方法．

(5)几个常用关系式

①sinα+cosα，sinα-cosα，sinα·cosα；(三式之间可以互相表示．)

同理可以由sinα-cosα或sinα·cosα推出其余两式．

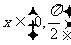②．　　　　 ③当时，有．

2．诱导公式

(1)诱导公式中的角是使公式成立的任意角．

(2)正确使用诱导公式的关键是公式中符号的确定．

(3)sin(kπ+α)=(-1)^ksinα；cos(kπ+α)=(-1)^kcosα(k∈Z)．

⑷熟记关系式；．

3．两角和与差的三角函数

(1)公式不但要会正用，还要会逆用．　　　　　　 (2)公式的变形应用要熟悉．

熟记：tanα+tanβ=tan(α+β)(1-tanα·tanβ)，它体现了两个角正切的和与积的关系．

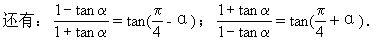
(3)角的变换要能灵活应用，如α=(α+β)-β，β=α-(α-β)，2α=(α+β)+(α-β)等．

4．倍角公式，半角公式

(2)使用二倍角的正弦、余弦公式时，公式的选择要准确．

如已知sinα，cosα，tanα求cos2α时，应分别选择cos2α=1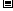

(3)余弦的二倍角公式的变形--升幂公式、降幂公式必须熟练掌握．要明确，降幂法是三角变换中非常重要的变形方法．

对sin3α，cos3α的公式应记住．

(4)使用正弦、余弦的半角公式时，要注意公式中符号的确定方法．正

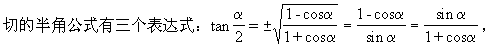
在使用无理表达式时，须要确定符号；在使用两个有理表达式时，无须确定符号，这是与选用无理表达式最大的区别，因此在化简、证明题中，

5．和差化积、积化和差公式，这两组公式现在不要求记忆，但要会使用．

(1)要明确，这两组公式是解决正、余弦的加、减、乘的运算关系式．

(3)对下列关系式要熟记：

6．三角变换：

三角函数式的恒等变形或用三角式来代换代数式称为三角变换．

三角恒等变形是以同角三角公式，诱导公式，和、差、倍、半角公式，和差化积和积化和差公式，万能公式为基础．

三角代换是以三角函数的值域为根据，进行恰如其分的代换，使代数式转化为三角式，然后再使用上述诸公式进行恒等变形，使问题得以解决．

7．三角形中的三角变换

三角形中的三角变换，除了应用上述公式和上述变换方法外，还要注意三角形自身的特点．

(1)角的变换

因为在△ABC中，A+B+C=π，所以

sin(A+B)=sinC；cos(A+B)=-cosC；tan(A+B)=-tanC．

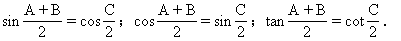
(2)三角形边、角关系定理及面积公式，正弦定理，余弦定理．

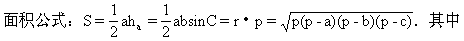
r为三角形内切圆半径，p为周长之半．

在非直角△ABC中，tanA+tanB+tanC=tanA·tanB·tanC．

(4)在△ABC中，熟记并会证明：

∠A，∠B，∠C成等差数列的充分必要条件是∠B=60°．

△ABC是正三角形的充分必要条件是∠A，∠B，∠C成等差数列且a，b，c成等比数列．

8．三角形的面积公式：

(1)△＝ah_a＝bh_b＝ch_c(h_a、h_b、h_c分别表示a、b、c上的高)．

(2)△＝absinC＝bcsinA＝acsinB．

(3)△＝＝＝．

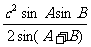(4)△＝2R²sinAsinBsinC． (R为外接圆半径)

(5)△＝．

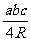(6)△＝；．

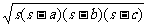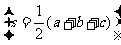(7)△＝r·s．

9．直角三角形中各元素间的关系：

如图，在△ABC中，C＝90°，AB＝c，AC＝b，BC＝a．

(1)三边之间的关系：a²+b²＝c²．(勾股定理)

(2)锐角之间的关系：A+B＝90°；

(3)边角之间的关系：(锐角三角函数定义)

sinA＝cosB＝，cosA＝sinB＝，

tgA＝ctgB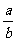＝，ctgA＝tgB＝．

10．斜三角形中各元素间的关系:

如图6-29，在△ABC中，A、B、C为其内角，a、b、c分别表示A、B、C的对边．

(1)三角形内角和：A+B+C＝π．

(2)正弦定理：在一个三角形中，各边和它所对角的正弦的比相等.

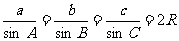
(R为外接圆半径)

(3)余弦定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍．

a²＝b²+c²－2bccosA，

b²＝c²+a²－2cacosB，

c²＝a²+b²－2abcosC．

(4)射影定理：a＝b·cosC+c·cosB，

b＝a·cosC+c·cosA，

c＝a·cosB+c·cosA．

11．解三角形：由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形．广义地，这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等．解三角形的问题一般可分为下面两种情形：若给出的三角形是直角三角形，则称为解直角三角形；若给出的三角形是斜三角形，则称为解斜三角形．

解斜三角形的主要依据是：

设△ABC的三边为a、b、c，对应的三个角为A、B、C．

(1)角与角关系：A+B+C = π，

(2)边与边关系：a + b > c，b + c > a，c + a > b，a－b < c，b－c < a，c－a > b．

(3)边与角关系：

正弦定理　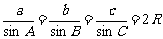 (R为外接圆半径)．

余弦定理　 c² = a²+b²－2bccosC，b² = a²+c²－2accosB，a² = b²+c²－2bccosA．

它们的变形形式有：a = 2R sinA，，．

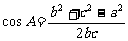(4)面积公式：

．

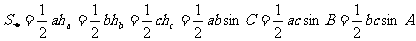解斜三角形的常规思维方法是：

(1)已知两角和一边(如A、B、C)，由A+B+C = π求C，由正弦定理求a、b．

(2)已知两边和夹角(如a、b、c)，应用余弦定理求c边；再应用正弦定理先求较短边所对的角，然后利用A+B+C = π，求另一角．

(3)已知两边和其中一边的对角(如a、b、A)，应用正弦定理求B，由A+B+C = π求C，再由正弦定理或余弦定理求c边，要注意解可能有多种情况．

(4)已知三边a、b、c，应余弦定理求A、B，再由A+B+C = π，求角C．

6．理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化．