14. 某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件，为了以后估计每个月的产量，以这三个月的产品数据为依据. 用一个函数模拟产品的月产量与月份数的关系，模拟函数可选用二次函数(其中为常数，且)或指数型函数(其中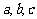为常数)，已知4月份该产品产量为1.37万件，请问用上述哪个函数模拟较好？说明理由.(☆P₅₁ 例2)

13. 家用冰箱使用的氟化物的释放破坏了大气上层臭氧层. 臭氧含量Q呈指数函数型变化，满足关系式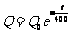，其中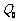是臭氧的初始量.　 (1)随时间的增加，臭氧的含量是增加还是减少？ (2)多少年以后将会有一半的臭氧消失？ (参考数据：)　 (☆P₄₄ 9)

12. 某商场经销一批进货单价为40元的商品，销售单价与日均销售量的关系如下表：

为了获取最大利润，售价定为多少时较为合理？ (☆P₄₉ 例1)

11. (1)已知函数图象是连续的，有如下表格，判断函数在哪几个区间上有零点. (☆P₄₀ 8)

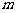(2)已知二次方程的两个根分别属于(-1,0)和(0,2),求的取值范围. (☆P₄₀ 9)

10. 对于函数.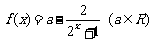

(1)探索函数的单调性；(2)是否存在实数a使得为奇函数.　 (◎P₉₁ B3)

9. 已知函数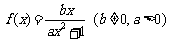.　　 (☆P₃₇ 例2)

(1)判断的奇偶性；　 (2)若，求a，b的值.

8. 已知函数其中．　 (◎P₈₄ 4)

(1)求函数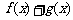的定义域；　　 (2)判断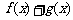的奇偶性，并说明理由；

(3)求使成立的的集合.　

7. 已知函数.　　 (☆P₁₆ 8题)

(1)证明在上是减函数;(2)当时，求的最大值和最小值.

6. 已知函数，求、、的值.(◎P₄₉ B4)

5. 已知函数.(1)求的定义域与值域(用区间表示)；(2)求证在上递减.