
22.(本小题满分10分)选修4-1:几何证明讲
 已知
已知 ABC中,AB=AC, D是
ABC中,AB=AC, D是 ABC外接圆劣弧
ABC外接圆劣弧 上的点(不与点A,C重合),延长BD至E。
上的点(不与点A,C重合),延长BD至E。
(1)。求证:AD的延长线平分 CDE;
CDE;
(2)。若 BAC=30,
BAC=30, ABC中BC边上的高为2+
ABC中BC边上的高为2+ ,
,
求 ABC外接圆的面积。
ABC外接圆的面积。
21.(本小题满分12分)
已知函数 (a>0).方程
(a>0).方程 有两个实根
有两个实根 .
.
(1).如果 ,函数
,函数 图象的对称轴是直线
图象的对称轴是直线 ,求证
,求证 ;
;
(2).如果 ,且
,且 的两实根之差为2,求实数b的取值范围.
的两实根之差为2,求实数b的取值范围.
★(请考生在以下二个题中任选一题作答,全答的以第一小题计分)
20. (本小题满分12分)
已知点(x, y) 在曲线C上,将此点的纵坐标变为原来的2倍,对应的横坐标不变,
得到的点满足方程 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线 在y轴上的截距
在y轴上的截距
为m(m≠0),直线 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.
(1)求曲线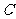 的方程;
(2)求m的取值范围.
的方程;
(2)求m的取值范围.
19. (本小题满分12分)
已知函数 为大于零的常数。
为大于零的常数。
(1)若函数 内调递增,求a的取值范围;
内调递增,求a的取值范围;
(2)求函数 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
18. (本小题满分12分)
已知 ,函数
,函数 在x∈
在x∈ 时的值恒为正.
时的值恒为正.
( 1 ). a的取值范围;
( 2 ). 记( 1 )中a的取值范围为集合A,函数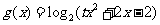 的定义域为集合B.若A∩B≠
的定义域为集合B.若A∩B≠ ,求实数t的取值范围.
,求实数t的取值范围.
满分70分。
17.(本小题满分12分)
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀
统计成绩后,得到如下的列联表.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按 的可靠性要求,能否认为“成绩与班级有关系”
的可靠性要求,能否认为“成绩与班级有关系”
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进
行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽
到6或10号的概率.
16.以下四个命题,是真命题的是 ____(把你认为是真命题的序号都填在横线上).
①若 在区间(1,2)有一个零点;
在区间(1,2)有一个零点;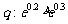 ,
, 为假命题;
为假命题;
②当 时,
时, ,
, ,
,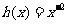 的大小关系是
的大小关系是 ;
;
③若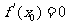 ,则
,则 在
在 处取得极值;
处取得极值;
④若不等式 的解集为
的解集为 ,函数y=
,函数y= 的定义域为
的定义域为 ,则“
,则“ ”是“
”是“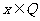 ”的充分不必要条件.
”的充分不必要条件.
15. 已知函数 (a>0),若
(a>0),若 ≤0恒成立,则a的取值范围是
≤0恒成立,则a的取值范围是
14. 已知函数
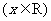 满足
满足 ,且
,且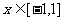 时,
时, ,
,
则 与
与 的图象的交点个数为
.
的图象的交点个数为
.
13. 若不等式
若不等式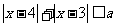 的解集为
的解集为 ,则
,则 的取值范围是
.
的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com