
3.C.解析:由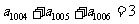 得
得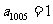 ,从而
,从而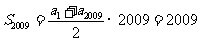 , 选C.若直接用通项公式和求和公式求解较复杂,解答中应用等差数列的性质
, 选C.若直接用通项公式和求和公式求解较复杂,解答中应用等差数列的性质 +
+  =
=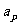 +
+  ,结论巧妙产生,过程简捷,运算简单.
,结论巧妙产生,过程简捷,运算简单.
2.B.解析:由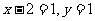 有
有 .
.
1.D.解析:依据定义,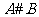 就是指将
就是指将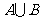 除去
除去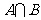 后剩余的元素所构成的集合;对于集合A,求的是函数
后剩余的元素所构成的集合;对于集合A,求的是函数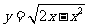 的定义域,解得:
的定义域,解得: ;对于集合B,求的是函数
;对于集合B,求的是函数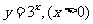 的值域,解得
的值域,解得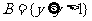 ;依据定义得:
;依据定义得: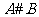 ={x|0≤x≤1或x>2}.
={x|0≤x≤1或x>2}.
21.(本小题满分14分)己知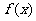 为二次函数,
为二次函数,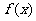 的导数记为
的导数记为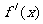 ,不等式
,不等式 的解集为
的解集为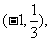 且对任意
且对任意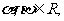 恒有
恒有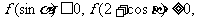 数列
数列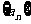 满足
满足
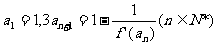 .
.
(Ⅰ)求函数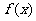 的解析式;
的解析式;
(Ⅱ)设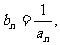 求数列
求数列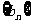 的通项公式;
的通项公式;
(Ⅲ)若(Ⅱ)中数列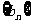 的前n项和为
的前n项和为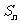 ,求数列
,求数列 的前
的前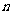 项和
项和 .
.
[答案及详细解析]
20.(本小题满分14分)在直角坐标平面上,O为原点,M为动点,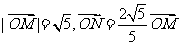 . 过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
. 过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,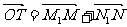 . 记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
. 记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在直线l,使得|BP|=|BQ|,并说明理由.
19.(本小题满分14分)民生问题是我国政府近一段时期的一个重点.据调查,某地区100
万从事传统农业的农民,人均收入3000元,为了增加农民的收入,当地政府积极引进资本,
建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,
据估计,如果有x(x>0)万人进企业工作,那么剩下从事传统农业的农民的人均收入有望提
高2x%,而进入企业工作的农民的人均收入为3000a元(a>0).
(I)在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工企业建立前的
农民的年总收入,试求x的取值范围;
(II)在(I)的条件下,当地政府应该如何引导农民(即x多大时),能使这100万农民的人均年收入达到最大.
18.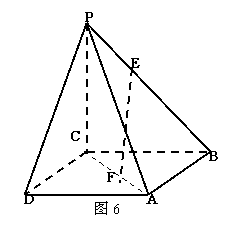 (本小题满分13分)如下图,在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图4),图5为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
(本小题满分13分)如下图,在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图4),图5为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
|

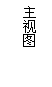

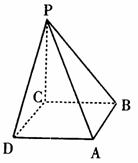
(Ⅰ) 根据图5所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面
图形的面积.
(Ⅱ)图6中,E为棱PB上的点,F为底面对角线AC上的点,且 ,求证:EF//平面PDA
.
,求证:EF//平面PDA
.
17.(本小题满分12分)为了了解某中学女生的身高情况,对九年级女生身高进行了一次测量,所得数据整理后列出了频率分布表如下
|
组别 |
频数 |
频率 |
|
145.5-149.5 |
1 |
0.02 |
|
149.5-153.5 |
4 |
0.08 |
|
153.5-157.5 |
20 |
0.40 |
|
157.5-161.5 |
15 |
0.30 |
|
161.5-165.5 |
8 |
0.16 |
|
165.5-169.5 |
m |
n |
|
合计 |
M |
N |
(Ⅰ)求出表中m、n,M、N所表示的数分别是多少?
(Ⅱ)画出频率分布直方图;
(Ⅲ)全体女生身高在哪组范围内的人数最多?估计九年级学生女生身高在161.5以上的概率.
16.(本小题满分13分)已知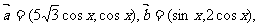 设函数
设函数
(Ⅰ)当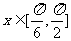 ,求函数
,求函数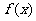 的的值域;
的的值域;
|
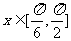 时,若
时,若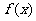 =8, 求函数
=8, 求函数 的值;
的值;
(Ⅲ)将函数y=f(x)的图象向右平移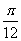 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数 的表达式并判断奇偶性.
的表达式并判断奇偶性.
(二)选做题(14-15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在直角坐标系中,参数方程为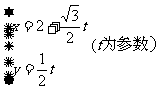 的
的
直线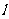 ,被以原点为极点、
,被以原点为极点、 轴的正半轴为极轴、极坐标方程为
轴的正半轴为极轴、极坐标方程为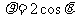 的曲线
的曲线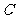 所截,
所截,
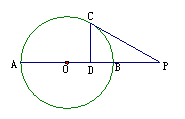 则得的弦长是
.
则得的弦长是
.
15.(几何证明选讲选做题)如图3,点P在圆O直径
AB的延长线上,且PB=OB=2,PC切圆O于C点,
CD AB于D点,则PC= ,CD= .
AB于D点,则PC= ,CD= .
图3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com