8．函数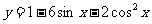的最小值是(　 )

A 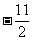．　 B．　 　　 C ．　　 　　　　　　 D．

7．某人欲购铅笔和圆珠笔共若干只，已知铅笔1元一只，圆珠笔2元一只．要求铅笔不超

过2只，圆珠笔不超过2只，但铅笔和圆珠笔总数不少于2只，则支出最少和最多的钱数

分别是(　 )

A．2元，6元　　 B．2元，5元　　 C．3元，6元　　　 D． 3元，5元

6．如图，一个几何体的三视图都是边长为1的正方形，那么这个几何体的体积为(　 )

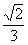　 A． 　　B．　 　　C．　 　D．1

5．关于函数函数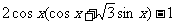，以下结论正确的是(　 )

A．的最小正周期是，在区间是增函数　　　

B．的最小正周期是，最大值是2　　　　

C．的最小正周期是，最大值是　　　　

D．的最小正周期是，在区间是增函数

4．双曲线的焦点在轴上，一条渐近线方程为，则双曲线的离心率为(　　 )

A．　　 B．　　 C ．　　　 D．

3．要完成下列两项调查：①从某社区125户高收入家庭、200户中等收入家庭、95户低收入家庭中选出100户，调查社会购买能力的某项指标；② 从某中学的5名艺术特长生中选出3名调查学习负担情况．宜采用的方法依次为(　　 )　

A．①简单随机抽样调查，②系统抽样　　 B．①分层抽样，②简单随机抽样　　　

　C．①系统抽样，②　 分层抽样　　　　　 D．①② 都用分层抽样

2．已知命题“若，则”，则命题及其逆命题、否命题、逆否命题中，正确命题的个数是(　 　)

A．1个　　 B．2个　　　　 C．3个　　　 D．4个

1．设复数是纯虚数，则=(　　 )

A．　　 B．　　 C ．　　　 D．　

16．设函数是定义域上的奇函数，则＝　　　　 .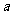

三解答题(74分)

17(12分)．已知{}是公比为q的等比数列，且成等差数列. 　 　　　

　 (Ⅰ)求q的值；

(Ⅱ)设{}是以2为首项，q为公差的等差数列，其前n项和为S_n，当n≥2时，比较S_n与b_n的大小，并说明理由.

18(12分)．已知函数，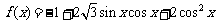

(1)求函数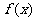的最小正周期；　 　　　

(2)求函数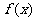的单调减区间；

							2
							1
x							0

(3)试列表描点画出函数的图象，由图象研究并写出的对称轴和对称中心.

19(12分)．已知函数

(Ⅰ)求的最小值；　 　　　

(Ⅱ)若对所有都有，求实数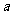的取值范围.

20(12分)．已知数列{}中，在直线y=x上，其中n=1,2,3….

(1)令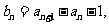求证数列是等比数列;

(2)求数列 　 　　　

21(12分)．已知角的顶点在原点，始边与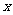轴的正半轴重合，终边经过点．

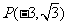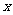(1)定义行列式 解关于的方程：；　 　　　

(2)若函数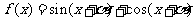()的图像关于直线对称,求的值．

22(14分)．设函数，，

其中|t|≤1，将f(x)的最小值记为g(t)．　 　　　

(1)求g(t)的表达式；

(2)对于区间[－1，1]中的某个t，是否存在实数a，使得不等式g(t)≤成立？如果存在，求出这样的a及其对应的t；如果不存在，请说明理由．

15．过原点作曲线的切线，则切线的斜率为　　　　 .