
05. --- Jim managed to get into his house without the key._______?
--- I don't know. He might have asked someone for help.
A. What for B. So what C. Guess how D. Who knows
04. The ______ amount of money was not known though they knew it was large.
A. real B. exact C. possible D. great
03. --- When did you last hear _______ Jay?
--- He phoned me this morning, and we agreed ______ a time and place to meet.
A. of; to B. about; with C. from; with D. from; on
02. Jack recommended me a few foreign movies, but _______ was to my taste.
A. all B. neither C. some D. none
第一节:单项填空(共20小题,每小题0.5分,满分10分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项标号涂黑。
01. Thank you for sending us ______ fresh vegetables of many kinds. You have done us ____ great service.
A. /;a B. the;a C. /;/ D. the;/
21.[解析](Ⅰ) ;
;
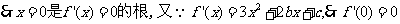 ,
,
 .…………………………………………………2分
.…………………………………………………2分
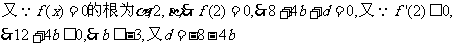
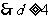 .………………………………………………4分
.………………………………………………4分
(Ⅱ) ………………5分
………………5分
 ,………………6分
,………………6分
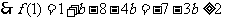 .………………………………8分
.………………………………8分
(Ⅲ)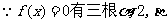 ;
;
 ;………………………………10分
;………………………………10分
 ………………12分
………………12分
 ·………………………………………………14分
·………………………………………………14分
20. [解析](Ⅰ)设直线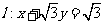 与椭圆
与椭圆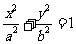 交于
交于 ,
,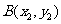 由
由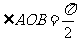 ,知
,知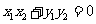 ,
………………………………………………………………2分
,
………………………………………………………………2分
而 代入上式得到
代入上式得到
 ; ……………………………………………………3分
; ……………………………………………………3分
而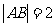 知
知 ,即
,即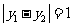 ;不妨设
;不妨设 则
则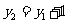 ………………5分
………………5分
 .
.

 或
或 ,或
,或 .
.
若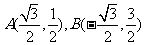 不合题意,舍去.………………………………7分
不合题意,舍去.………………………………7分
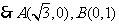 ,则椭圆方程为
,则椭圆方程为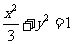 ,
,
故所求椭圆方程为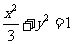 ……………………………………………………8分
……………………………………………………8分
(Ⅱ)
 是椭圆
是椭圆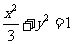 上的点,且
上的点,且 ,
,
故设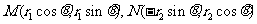 . ………………………… 10分
. ………………………… 10分
于是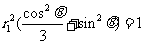
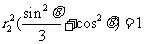 ,
,
从而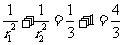 .…………………………………………………………12分
.…………………………………………………………12分
又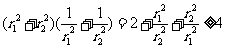 ,从而
,从而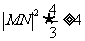 即
即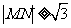 ,
,
故所求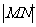 的最小值为
的最小值为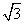 .…………………………………………… 14分
.…………………………………………… 14分
19.[解析] (Ⅰ)证明:
(Ⅰ)证明:
 ,
, ;
;
∴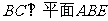 ,则
,则 . ……………2分
. ……………2分
又
 ,则
,则 ;
;
∴ . ……………4分
. ……………4分
(Ⅱ)证明:依题意可知 是
是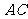 中点;
中点;

 则
则 ,而
,而 ,
,
∴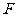 是
是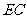 中点. ……………6分
中点. ……………6分
在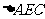 中,
中,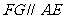 ,
,
∴ .
……………8分
.
……………8分
(Ⅲ)解:
 ,
,
∴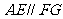 ,而
,而 .
.
∴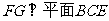 ∴
∴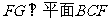 .……………-10分
.……………-10分

 是
是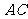 中点,
中点,
∴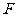 是
是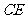 中点 , ∴
中点 , ∴
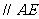 且
且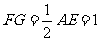 .
.

 , ∴
, ∴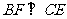 ; ∴
; ∴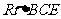 中,
中,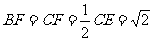 ;
;
∴ . ------12分
. ------12分
∴ . ……………13分
. ……………13分
18. [解析](Ⅰ)由题意规律,编号为2的同学看到的像是(6,8);
编号为3的同学看到的像是(8,11).…………………………………………4分
(Ⅱ)设编号为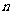 的同学看到的像是
的同学看到的像是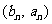 ,则
,则 ,
,
当 时,
时,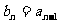 .…………………………………………………………5分
.…………………………………………………………5分
由题意 , ∴
, ∴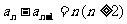 .…………………………6分
.…………………………6分
∴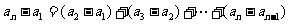 =
= =
=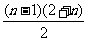 .…10分
.…10分
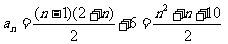 ,
, .………………12分
.………………12分
经检验 时,上式也成立.
时,上式也成立.
∴编号为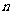 的同学看到的像是
的同学看到的像是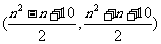 .………………………………13分
.………………………………13分
17.[解析](Ⅰ)设事件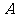 为“方程
为“方程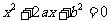 有实根”.
有实根”.
当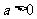 ,
,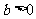 时,方程
时,方程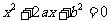 有实根的充要条件为
有实根的充要条件为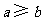 .………………2分
.………………2分
基本事件共12个:
 .其中第一个数表示
.其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值.……………………………………………………………………………4分
的取值.……………………………………………………………………………4分
事件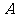 中包含9个基本事件,即
中包含9个基本事件,即
(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)……………6分
所以事件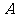 发生的概率为
发生的概率为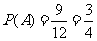 .…………………………………………………………7分
.…………………………………………………………7分
(Ⅱ)试验的全部结果所构成的区域为 ,……………………9分.
,……………………9分.
构成事件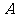 的区域为
的区域为 ,………………………………11分
,………………………………11分
所以所求的概率为 .………………………………………………………13分
.………………………………………………………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com