
17.(本小题满分12分)
本次高三数学月考试卷中共有8个选择题,每小题都有4个选项,其中有且只有一个选项是正确的,选对得5分,不选或选错都得0分.某同学对每道题都选出了一个答案,已确定第1-4题的答案都是正确的,对第5、6两道题,他都可判断出其中有两个选项是错误的,但对另两个选项都不能确定哪个正确;对第7题,他可判断出其中一个选项是错误的,但对另三个选项不能确定哪个正确;对第8题,他不理解题意只能乱猜,且各题答对与否相互独立.
(Ⅰ)求该同学在这次月考中选择题至少答对7道题的概率;
(Ⅱ)估计该同学在这次月考中选择题的实际得分最有可能是多少分?
[解](Ⅰ)设该同学在这次月考中选择题“答对8道题”为事件A,“答对7道题”为事件B,则事件A与B互斥. (1分)
据题意,第1-4题都答对为必然事件,第5、6题答对的概率都为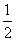 ,第7题答对的概率为
,第7题答对的概率为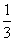 ,
,
第8题答对的概率为 ,且各题答对与否相互独立.
(2分)
,且各题答对与否相互独立.
(2分)
所以 .
(3分)
.
(3分)
 .
(5分)
.
(5分)
 .
.
故该同学在这次月考中选择题至少答对7道题的概率是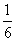 .
(6分)
.
(6分)
(Ⅱ)设该同学在这次月考中选择题的总得分为ξ分,则ξ的可能取值为20,25,30,35,40.
(7分)
若ξ=20,则只答对第1-4题,其余各题都答错,所以 . (8分)
. (8分)
若ξ=25,则第5-8题只答对1题,
所以 .
(9分)
.
(9分)
若ξ=30,则第5-8题只答对2题,
 .(10分)
.(10分)
由(Ⅰ)知, ,
,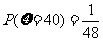 .
.
所以 .
(11分)
.
(11分)
估计该同学在这次月考中选择题的实际得分最有可能是30分. (12分)
16.(本小题满分12分)
在△ABC中,已知AB=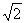 ,BC=1,cosC=
,BC=1,cosC= .
.
(Ⅰ)求sinA的值;
(Ⅱ)求 的值.
的值.
[解](Ⅰ)因为cosC= ,则sinC=
,则sinC=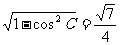 .
(3分)
.
(3分)
据正弦定理,有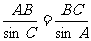 ,所以sinA=
,所以sinA=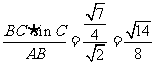 .
(6分)
.
(6分)
(Ⅱ)由余弦定理,得 .
.
设AC=b,则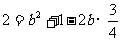 ,即
,即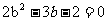 .
(8分)
.
(8分)
解得b=2或b=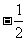 (舍去),AC=2.
(9分)
(舍去),AC=2.
(9分)
故 .
(12分)
.
(12分)
15.对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“科比函数”.
(1)给出下列两个函数:①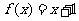 ;②
;② ,其中是“科比函数”的函数序号是 ② .
,其中是“科比函数”的函数序号是 ② .
(2)若函数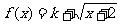 是“科比函数”,则实数k的取值范围是
是“科比函数”,则实数k的取值范围是 .
.
[解](1)因为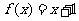 是增函数,若f(x)为“科比函数”,则f(a)=a,f(b)=b,即
是增函数,若f(x)为“科比函数”,则f(a)=a,f(b)=b,即
a+1=a,b+1=b,无解,所以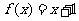 不是“科比函数”.
不是“科比函数”.
因为当x∈[0,1]时, ∈[0,1],所以
∈[0,1],所以 是“科比函数”.
是“科比函数”.
(2)因为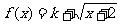 是增函数,若
是增函数,若 是“科比函数”,则存在实数a,b(-2≤a<b),使
是“科比函数”,则存在实数a,b(-2≤a<b),使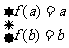 ,即
,即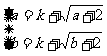 .所以a,b为方程
.所以a,b为方程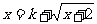 的两个实数根,从而方程
的两个实数根,从而方程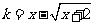 有两个不等实根.
有两个不等实根.
令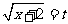 ,则
,则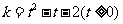 .当t=0时,k=-2;当t=
.当t=0时,k=-2;当t=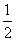 时,k=
时,k= .
.
由图可知,当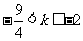 时,直线y=k与曲线
时,直线y=k与曲线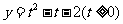 有两个不同交点,即方程
有两个不同交点,即方程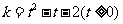 有两个不等实根,故实数k的取值范围是
有两个不等实根,故实数k的取值范围是 .
.
14.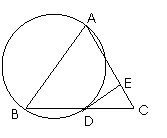 如图,在△ABC中,AB=AC=4,BC=6,以AB为直径的圆交BC于点D,过点D作该圆的切线,交AC于点E,则CE=
如图,在△ABC中,AB=AC=4,BC=6,以AB为直径的圆交BC于点D,过点D作该圆的切线,交AC于点E,则CE=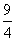 .
.
[解]设圆心为O,连结OD,AD,则OD⊥DE,AD⊥BC.
因为AB=AC,所以D为BC的中点,从而OD是△ABC的
中位线,所以OD∥AC,于是AC⊥DE.
在Rt△ADC中,由射影定理,得CD2=CE·CA.
因为CD=3,CA=4,所以CE=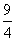 .
.
13.某饮料店的日销售收入y(单位:百元)与当天平均气温x(单位:°C)之间有下列数据:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
5 |
4 |
2 |
2 |
1 |
甲、乙、丙三位同学对上述数据进行了研究,分别得到了x与y之间的三个线性回归方程:
① ;②
;② ;③
;③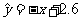 ,其中正确方程的序号是 ② .
,其中正确方程的序号是 ② .
[解]因为 ,
,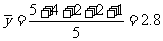 .
.
由于回归方程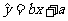 必过点(
必过点( ),将点(0,2.8)逐一代入验证得,方程②满足要求.
),将点(0,2.8)逐一代入验证得,方程②满足要求.
12.已知实数x,y满足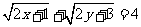 ,由柯西不等式可得x+y的最小值为 2 .
,由柯西不等式可得x+y的最小值为 2 .
[解]由柯西不等式,得 ,即
,即
 ,所以x+y≥2.当且仅当
,所以x+y≥2.当且仅当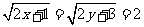 ,即
,即 时等号成立,故x+y的最小值为2.
时等号成立,故x+y的最小值为2.
11.已知平面向量a,b,c满足:a⊥c,b·c=-2,|c|=2,若存在实数λ使得c=a+λb,则λ的值为 -2 .
[解]由已知,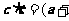
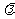
 ,即
,即 =
= +
+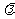
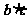 .
.
又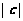 =2,
=2, =0,
=0,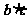 =-2,所以-2
=-2,所以-2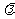 =4,即
=4,即 .
.
10.某企业在今年九月生产了A、B、C三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下统计表格:
|
产品类别 |
A |
B |
C |
|
产品数量(件) |
 |
1300 |
|
|
样本容量 |
|
130 |
|
由于统计员不小心,表格中A、C产品的有关数据已被污染看不清楚,但统计员记得A产品的样本容量比C产品的样本容量多10件.根据以上信息,可得C产品的数量是 800 件.
[解]设C产品的样本容量为,因为抽样比例为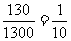 ,则
,则
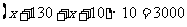 ,解得
,解得 .所以C产品的数量是
.所以C产品的数量是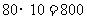 件.
件.
9.已知集合 ,
, ,若
,若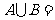 R,则实数的取值范围是 (1,5)
.
R,则实数的取值范围是 (1,5)
.
[解]由已知可得, ,
, .
.
因为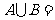 R,则
R,则 ,即
,即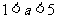 ,故的取值范围是(1,5).
,故的取值范围是(1,5).
8.如图,一个质点从原点出发,在x轴、y轴的平行方向按
(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)→…
的规律向前移动,且每秒钟移动一个单位长度,那么到第
2009秒时,这个质点所处位置的坐标是 ( B )
A. (14,44) B. (15,44)
C. (44,14) D. (44,15)
[解]由图可知,质点走完一个矩形回路所走路程依次为
3,5,7,…,(2n+1)个单位长度.
由3+5+7+…+(2n+1)<2009,得n≤43.当质点走完第43个正方形时,共走了1935个单位长度,余下74个单位长度从(43,0)→(44,44)有45个单位,再向左走29个单位即可,此时质点的坐标为(15,44),故选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com