
6. 在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )

5.函数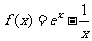 的零点所在的区间是( )
的零点所在的区间是( )
A.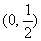 B.
B.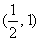 C.
C. D.
D.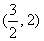
4.给出下面的程序框图,那么输出的数是 ( )
A.2450 B. 2550 C. 5050 D. 4900
3. 如果复数 的实部与虚部互为相反数,则
的实部与虚部互为相反数,则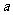 的值等于
的值等于
A.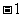 B.
B.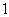 C.
C.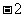 D.
D.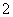
2.如果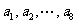 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差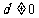 ,则( )
,则( )
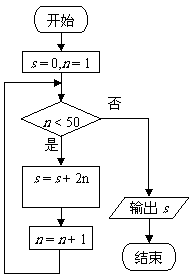 A.
A. B.
B.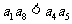 C.
C.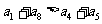 D.
D.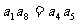
1.已知集合P={ 0,m },Q={x│ },若P∩Q
≠
},若P∩Q
≠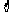 ,则m等于 ( )
,则m等于 ( )
(A) 1 (B) 2
(C) 1或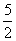 (D)1或2
(D)1或2
21.(本小题满分13分)
已知数列 是首项为,公差为
是首项为,公差为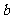 的等差数列,
的等差数列, 是首项为
是首项为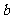 ,公比为的等比数列,且满足
,公比为的等比数列,且满足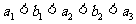 ,其中
,其中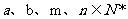 .
.
(Ⅰ)求的值;
(Ⅱ)若数列 与数列
与数列 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列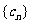 ,求数列
,求数列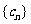 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列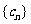 的前项之和为
的前项之和为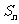 ,求证:
,求证:
 .
.
[解](Ⅰ)由题设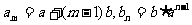 .
(1分)
.
(1分)
由已知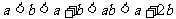 ,所以
,所以 .又b>0,所以a<3. (2分)
.又b>0,所以a<3. (2分)
因为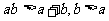 ,则
,则 .又a>0,所以b>2,从而有
.又a>0,所以b>2,从而有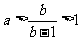 . (3分)
. (3分)
因为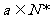 ,故
,故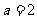 .
(4分)
.
(4分)
(Ⅱ)设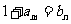 ,即
,即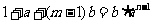 .
(5分)
.
(5分)
因为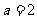 ,则
,则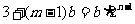 ,所以
,所以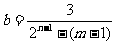 .
(6分)
.
(6分)
因为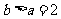 ,且b∈N*,所以
,且b∈N*,所以 ,即
,即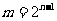 ,且b=3.
(7分)
,且b=3.
(7分)
故 .
(8分)
.
(8分)
(Ⅲ)由题设,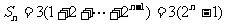 .
(9分)
.
(9分)
当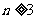 时,
时,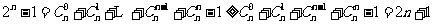 ,当且仅当
,当且仅当 时等号成立,所以
时等号成立,所以 .
(11分)
.
(11分)
于是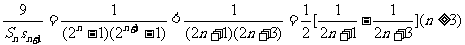 . (12分)
. (12分)
因为S1=3,S2=9,S3=21,则



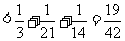 .
(13分)
.
(13分)
20.(本小题满分13分)
如图,抛物线的顶点O在坐标原点,焦点在y轴负半轴上,过点M(0,-2)作直线l与抛物线相交于A,B两点,且满足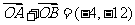 .
.
(Ⅰ)求直线l和抛物线的方程;
(Ⅱ)当抛物线上一动点P从点A到B运动时,求△ABP面积的最大值.
 [解](Ⅰ)据题意可设直线l的方程为
[解](Ⅰ)据题意可设直线l的方程为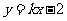 ,
,
抛物线方程为 .
(2分)
.
(2分)
由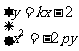 得,
得,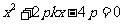 .
(3分)
.
(3分)
设点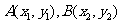 ,则
,则
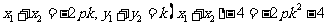 .
.
所以 .
(4分)
.
(4分)
因为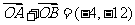 ,所以
,所以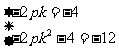 ,解得
,解得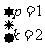 .
(5分)
.
(5分)
故直线 的方程为
的方程为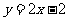 ,抛物线方程为
,抛物线方程为 (6分)
(6分)
(Ⅱ)解法一:据题意,当抛物线过点P的切线与 平行时,△APB面积最大. (7分)
平行时,△APB面积最大. (7分)
设点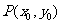 ,因为
,因为 ,由
,由 ,
,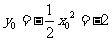 ,所以
,所以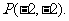
(9分)
此时,点P到直线 的距离
的距离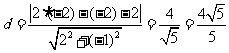 .
(10分)
.
(10分)
由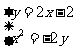 ,得
,得 .
(11分)
.
(11分)
所以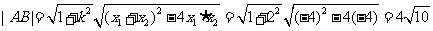 .
(12分)
.
(12分)
故△ABP面积的最大值为 .
(13分)
.
(13分)
解法二:由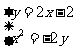 得,
得, .
(7分)
.
(7分)
所以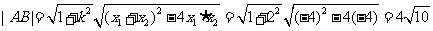 .
(8分)
.
(8分)
设点
 ,点P到直线
,点P到直线 的距离
的距离 .
(9分)
.
(9分)
则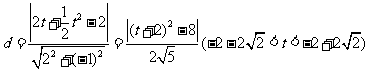 ,
,
当 时,
时, max=
max=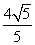 ,此时点
,此时点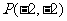 .
(12分)
.
(12分)
故△ABP面积的最大值为 .
(13分)
.
(13分)
19.(本小题满分13分)
某地需要修建一条大型输油管道通过120公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为432万元,铺设距离为公里的相邻两增压站之间的输油管道费用为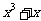 万元.设余下工程的总费用为万元.
万元.设余下工程的总费用为万元.
(Ⅰ)试将表示成关于的函数;
(Ⅱ)需要修建多少个增压站才能使最小?
[解](I)设需要修建 个增压站,则
个增压站,则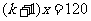 ,即
,即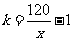 .
(2分)
.
(2分)
所以 .(5分)
.(5分)
因为x表示相邻两增压站之间的距离,则0<x≤120. (6分)
故y与x的函数关系是 .
(7分)
.
(7分)
(II)设 ,则
,则
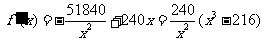 .
(9分)
.
(9分)
由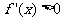 ,得
,得 ,又0<x≤120,则
,又0<x≤120,则 .
(10分)
.
(10分)
所以 在区间
在区间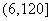 内为增函数,在区间
内为增函数,在区间 内为减函数.
(11分)
内为减函数.
(11分)
所以当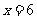 时,
时, 取最小值,此时
取最小值,此时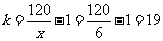 .
(12分)
.
(12分)
故需要修建19个增压站才能使最小. (13分)
18.(本小题满分12分)
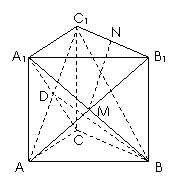
 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
(Ⅰ)求证:MN⊥平面A1BC;
(Ⅱ)求直线BC1和平面A1BC所成角的大小.
[解]解法一:(Ⅰ)由已知BC⊥AC,BC⊥CC1,
所以BC⊥平面ACC1A1.连结AC1,则BC⊥AC1. (2分)
由已知,侧面ACC1A1是正方形,所以A1C⊥AC1. (3分)
又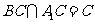 ,所以AC1⊥平面A1BC.
(4分)
,所以AC1⊥平面A1BC.
(4分)
因为侧面ABB1A1是正方形,M是A1B的中点,连结AB1,则点M是AB1的中点. (5分)
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.
 故MN⊥平面A1BC.
(6分)
故MN⊥平面A1BC.
(6分)
(Ⅱ)因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
连结BD,则∠C1BD为直线BC1和平面A1BC所成角. (9分)
设AC=BC=CC1=a,则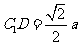 ,
,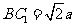 .
(10分)
.
(10分)
在Rt△BDC1中,sin∠C1BD= ,
(11分)
,
(11分)
所以∠C1BD=30º,故直线BC1和平面A1BC所成的角为30º. (12分)
 解法二:(Ⅰ)据题意CA、CB、CC1两两垂直,以C为原点,
解法二:(Ⅰ)据题意CA、CB、CC1两两垂直,以C为原点,
CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间
直角坐标系,如图. (2分)
设AC=BC=CC1=a,则
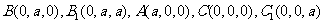 ,
,
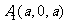 ,
, .
(4分)
.
(4分)
所以 ,
,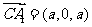 ,
,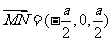 .
(5分)
.
(5分)
于是 ,
, ,即MN⊥BA1,MN⊥CA1.
(6分)
,即MN⊥BA1,MN⊥CA1.
(6分)
又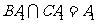 ,故MN⊥平面A1BC.
(7分)
,故MN⊥平面A1BC.
(7分)
(Ⅱ)因为MN⊥平面A1BC,则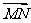 为平面A1BC的法向量,又
为平面A1BC的法向量,又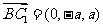 , (9分)
, (9分)
则 ,所以
,所以 . (11分)
. (11分)
故直线BC1和平面A1BC所成的角为30º. (12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com