
21.(本小题满分13分)
设数列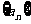 的各项都为正数,其前项和为
的各项都为正数,其前项和为 ,已知对任意
,已知对任意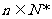 ,
, 是
是 和
和 的等差中项.
的等差中项.
(Ⅰ)证明数列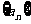 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)证明 ;
;
(Ⅲ)设集合 ,
,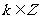 ,且
,且 ,若存在∈M,使对满足
,若存在∈M,使对满足 的一切正整数,不等式
的一切正整数,不等式 恒成立,求这样的正整数共有多少个?
恒成立,求这样的正整数共有多少个?
[解](Ⅰ)由已知, ,且
,且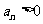 .
(1分)
.
(1分)
当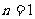 时,
时, ,解得
,解得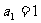 .
(2分)
.
(2分)
当 时,有
时,有 .
.
于是 ,即
,即 .
.
于是 ,即
,即 .
.
因为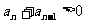 ,所以
,所以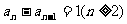 .
(4分)
.
(4分)
故数列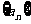 是首项为,公差为的等差数列,且
是首项为,公差为的等差数列,且 .
(5分)
.
(5分)
(Ⅱ)因为 ,则
,则 .
(7分)
.
(7分)
所以 2(
2( . (9分)
. (9分)
(Ⅲ)由 ,得
,得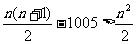 ,即
,即 ,所以
,所以 . (10分)
. (10分)
由题设, ,
,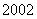 ,…,
,…,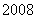 ,
, ,
, ,…,
,…,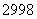
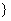 ,因为∈M,
,因为∈M,
所以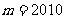 ,
, ,…,
,…,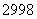 均满足条件,且这些数组成首项为
均满足条件,且这些数组成首项为 ,公差为的等差数列.
(12分)
,公差为的等差数列.
(12分)
设这个等差数列共有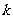 项,则
项,则 ,解得
,解得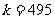 .
.
故集合M中满足条件的正整数共有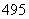 个.
(13分)
个.
(13分)
20.(本小题满分13分)
已知抛物线C的顶点在坐标原点,焦点在x轴上,P(2,0)为定点.
(Ⅰ)若点P为抛物线的焦点,求抛物线C的方程;
(Ⅱ)若动圆M过点P,且圆心M在抛物线C上运动,点A、B是圆M与轴的两交点,试推断是否存在一条抛物线C,使|AB|为定值?若存在,求这个定值;若不存在,说明理由.
[解](Ⅰ) 设抛物线方程为 ,则抛物线的焦点坐标为
,则抛物线的焦点坐标为 . (2分)
. (2分)
由已知, ,即
,即 ,故抛物线C的方程是
,故抛物线C的方程是 .
(4分)
.
(4分)
(Ⅱ)设圆心 (
(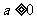 ),点A
),点A ,B
,B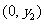 .
(5分)
.
(5分)
因为圆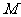 过点P(2,0),则可设圆M的方程为
过点P(2,0),则可设圆M的方程为 .
(6分)
.
(6分)
令 ,得
,得 .
(7分)
.
(7分)
则 ,
, .
(8分)
.
(8分)
所以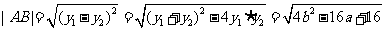 .
(9分)
.
(9分)
设抛物线C的方程为 ,因为圆心M在抛物线C上,则
,因为圆心M在抛物线C上,则 .
(10分)
.
(10分)
所以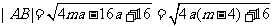 .
(11分)
.
(11分)
由此可得,当 时,
时, 为定值.
(12分)
为定值.
(12分)
故存在一条抛物线 ,使|AB|为定值4.
(13分)
,使|AB|为定值4.
(13分)
19.(本小题满分13分)
某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为公里的相邻两增压站之间的输油管道费用为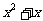 万元.设余下工程的总费用为万元.
万元.设余下工程的总费用为万元.
(Ⅰ)试将表示成关于的函数;
(Ⅱ)需要修建多少个增压站才能使最小,其最小值为多少万元?
[解](I)设需要修建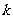 个增压站,则
个增压站,则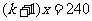 ,即
,即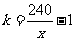 .
(2分)
.
(2分)
所以 .(5分)
.(5分)
因为x表示相邻两增压站之间的距离,则0<x≤240. (6分)
故y与x的函数关系是 .
(7分)
.
(7分)
(II) . (10分)
. (10分)
当且仅当 即
即  时取等号.此时,
时取等号.此时,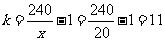 . (12分)
. (12分)
故需要修建11个增压站才能使最小,其最小值为9440万元. (13分)
18.(本小题满分12分)
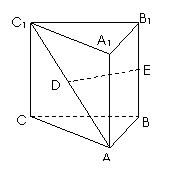 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=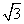 ,D,E分别是AC1和BB1的中点.
,D,E分别是AC1和BB1的中点.
(Ⅰ)证明:DE∥平面ABC;
(Ⅱ)求直线DE与平面BB1C1C所成的角.
[解](Ⅰ)取AC的中点F,连结DF,BF.
则FD∥CC1,且 .
(2分)
.
(2分)
因为BB1∥CC1,E是BB1的中点,
所以BE∥CC1,且 .
(4分)
.
(4分)
 于是FD∥BE,且FD=BE,所以四边形BEDF是
于是FD∥BE,且FD=BE,所以四边形BEDF是
平行四边形,从而DE∥FB. (5分)
又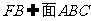 ,故DE∥平面ABC.
(6分)
,故DE∥平面ABC.
(6分)
(Ⅱ)连结BC1,取BC1的中点M,连结DM,EM.
因为D为AC1的中点,所以DM∥AB.
(7分)
由AB=1,AC=2,BC=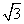 ,可知AB⊥BC.又AB⊥BB1,所以AB⊥面BB1C1C. (9分)
,可知AB⊥BC.又AB⊥BB1,所以AB⊥面BB1C1C. (9分)
从而DM⊥面B1C1CB,故∠DEM为直线DE与平面BB1C1C所成的角. (10分)
在Rt△DME中,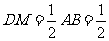 ,EM=
,EM=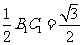 ,所以
,所以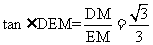 .
.
故∠DEM=30º,即直线DE与平面BB1C1C所成的角为30º. (12分)
17.(本小题满分12分)
 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的月均用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下,其中直方图从左到右前3个小矩形的面积之比为1︰2︰3,试估计:
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的月均用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下,其中直方图从左到右前3个小矩形的面积之比为1︰2︰3,试估计:
(Ⅰ)该乡镇月均用电量在39.5-43.5内
的居民所占百分比约是多少?
(Ⅱ)该乡镇居民月均用电量的中位数约是
多少?(精确到0.01)
[解](Ⅰ)设直方图从左到右前3个小矩形的面积分别为P,2P,3P.
由直方图可知,最后两个小矩形的面积之和为(0.0875+0.0375)×2=0.25. (2分)
因为直方图中各小矩形的面积之和为1,所以P+2P+3P=0.75,即P=0.125. (4分)
所以3P+0.0875×2=0.55.
由此估计,该乡镇居民月均用电量在39.5-43.5内的居民所占百分比约是55%. (6分)
(Ⅱ)显然直方图的面积平分线位于正中间一个矩形内,且该矩形在面积平分线左侧部分的面积为0.5-P-2P=0.5-0.375=0.125, (8分)
设样本数据的中位数为39.5+x.
因为正中间一个矩形的面积为3P=0.375,所以x︰2=0.125︰0.375,即x= ≈0.67.(10分)
≈0.67.(10分)
从而39.5+x≈40.17, 由此估计,该乡镇居民月均用电量的中位数约是40.17(kw/h).(12分)
16.(本小题满分12分)
在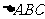 中,已知
中,已知 .
.
(Ⅰ) 求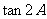 的值;
的值;
(Ⅱ) 若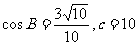 ,求
,求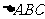 的面积.
的面积.
[解](Ⅰ)因为sin(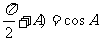 ,由已知,
,由已知,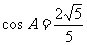 .
(2分)
.
(2分)
因为角A是△ABC内角,且cosA>0,则角A是锐角.
所以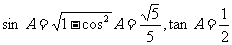 .
(4分)
.
(4分)
故 .
(6分)
.
(6分)
(Ⅱ)因为 ,B为三角形的内角,所以
,B为三角形的内角,所以 .
(7分)
.
(7分)
于是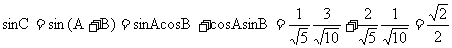 . (9分)
. (9分)
因为c=10,由正弦定理,得 .
(11分)
.
(11分)
故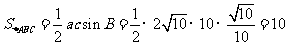 .
(12分)
.
(12分)
15.某计算装置有一个数据入口A和一个运算出口B,从入口A输入一个正整数n时,计算机通过循环运算,在出口B输出一个运算结果,记为f(n).计算机的工作原理如下: 为默认值,f(n+1)的值通过执行循环体“f(n+1)=
为默认值,f(n+1)的值通过执行循环体“f(n+1)=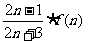 ”后计算得出.则f(2)=
”后计算得出.则f(2)=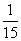 ;
;
当从入口A输入的正整数n=__12__时,从出口B输出的运算结果是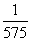 .
.
[解]由题设,f(n+1)=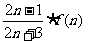 ,所以f(2)=
,所以f(2)=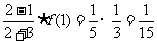 .
.
设从A口输入的最后一个正整数为n,因为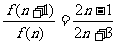 ,则
,则
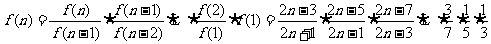
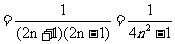 .
.
令4n2-1=575,则n2=144,即n=12.
14.已知圆C经过点A(2,-1),圆心在直线2x+y=0上,且与直线x+y=1相切,则圆C的标准方程是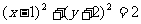 .
.
[解]因为圆心C在直线2x+y=0上,可设圆心为C(a,-2a).
则点C到直线x+y=1的距离 .
.
据题意, ,则
,则 ,解得
,解得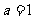 .
.
所以圆心为C(1,-2),半径 ,故所求圆的方程是
,故所求圆的方程是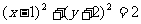 .
.
13. 甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作回归分析,分别求得相关系数r与残差平方和 如下表:
如下表:
|
|
甲 |
乙 |
丙 |
丁 |
|
r |
0.82 |
0.78 |
0.69 |
0.85 |
 |
106 |
115 |
124 |
103 |
则这四位同学中,其中 丁 同学的分析结果体现出A,B两变量具有更强的线性相关性.
[解]因为 越小表明回归方程预报精度越高,|r|越大表明线性相关性越强.由表可知,应填丁同学.
越小表明回归方程预报精度越高,|r|越大表明线性相关性越强.由表可知,应填丁同学.
12.已知向量a,b满足|a|=|b|=1,且|a+b|=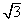 |a-b|,则向量a与b的夹角是 60°
.
|a-b|,则向量a与b的夹角是 60°
.
[解]由已知,(a+b)2=3(a-b)2,即a2+2a·b+b2=3(a2-2a·b+b2).
因为|a|=|b|=1,则a2=b2=1,所以2+2a·b=3(2-2a·b),即a·b= .
.
设向量a与b的夹角为θ,则|a|·|b|cosθ= ,即cosθ=
,即cosθ= ,故θ=60°.
,故θ=60°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com