
20.(本题满分12分)先后随机投掷2枚正方体骰子,其中 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数,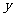 表示第
表示第 枚骰子出现的点数.
枚骰子出现的点数.
(1)求点 在直线
在直线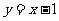 上的概率;
上的概率;
(2)求点 满足
满足 的概率.
的概率.
19.(本题满分12分)已知定义在R上的函数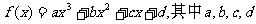 是实数.
是实数.
(1)若函数 在区间
在区间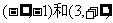 上都是增函数,在区间
上都是增函数,在区间 上是减函数,并且
上是减函数,并且 求函数
求函数 的表达式;
的表达式;
(2)若 ,求证:函数
,求证:函数 是单调函数.
是单调函数.
18.(本小题满分12分)已知各项均为正数的数列{ }的前n项和满足
}的前n项和满足 ,且
,且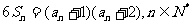
(1)求a1;
(2)证明{ }是等差数列并求数列的通项公式。
}是等差数列并求数列的通项公式。
17.(本小题满分10分).记函数 的定义域为A,
的定义域为A, 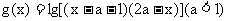 的定义域为B.
的定义域为B.
(1) 求集合A;
(2) 若 , 求实数
, 求实数 的取值范围.
的取值范围.
16.已知:给出下列命题:
① ; ②函数
; ②函数 的单调递减区间为
的单调递减区间为
③已知 :
: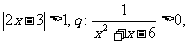 则
则 是
是 的必要不充分条件;
的必要不充分条件;
④在平面内,与两圆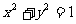 及
及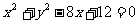 都外切的动圆圆心的轨迹是双曲线其中所有正确命题的序号为
都外切的动圆圆心的轨迹是双曲线其中所有正确命题的序号为
15.函数 在
在 上恒有
上恒有 ,则
,则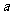 的取值范围是
的取值范围是
14.在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,若
,若 ,则
,则 的值等于
的值等于
13.若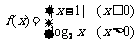 ,则
,则 .
.
12.已知 ,且对任意
,且对任意 都有
都有
①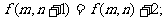 ②
② 。
。
则 的值为(
)
的值为(
)
A. B.
B. C.
C. D.
D.
第Ⅱ卷(非选择题,共90分)
11.设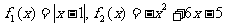 ,函数
,函数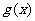 是这样定义的:当
是这样定义的:当 ,若方程
,若方程 有四个不同的实数解,则实数
有四个不同的实数解,则实数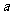 的取值范围是(
)
的取值范围是(
)
A.3<a<4 B.0<a<4 C.0<a<3 D.a<4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com