7.2.1古典概型

第32课时

知识网络

基本事件等可能事件古典概型

计算公式．

学习要求

3、如果某种彩票中奖的概率为，那么买1000张彩票一定能中奖吗？请用概率的意义解释。

2、下表是某种油菜子在相同条件下的发芽试验结果表，请完成表格并回答题。

(1)完成上面表格：

(2)该油菜子发芽的概率约是多少？

1、下列说法正确的是(　　 )

A．任一事件的概率总在(0，1)内　　

B．不可能事件的概率不一定为0

C．必然事件的概率一定为1

D．以上均不对

3.(1)频率的稳定性　 即大量重复试验时，任何结果(事件)出现的频率尽管是随机的，却“稳定”在某一个常数附近，试验的次数越多，频率与这个常数的偏差大的可能性越小，这一常数就成为该事件的概率;

(2)“频率”和“概率”这两个概念的区别是：频率具有随机性，它反映的是某一随机事件出现的频繁程度，它反映的是随机事件出现的可能性；概率是一个客观常数，它反映了随机事件的属性.

[经典范例]

例1　 某射手在同一条件下进行射击，结果如下表所示：

(1)填写表中击中靶心的频率；

(2)这个射手射击一次，击中靶心的概率约是什么？

例2　 某人进行打靶练习，共射击10次，其中有2次中10环，有3次环中9环，有4次中8环，有1次未中靶，试计算此人中靶的概率，假设此人射击1次，试问中靶的概率约为多大？中10环的概率约为多大？

例3　 在一场乒乓球比赛前，裁判员利用抽签器来决定由谁先发球，请用概率的知识解释其公平性。

追踪训练

2．概率的性质：

①随机事件的概率为，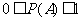

②必然事件和不可能事件看作随机事件的两个特例，分别用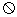和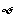表示，必然事件的概率为，不可能事件的概率为，即，;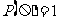

1.概率： 一般地，如果随机事件在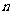次试验中发生了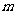次，当试验的次数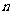很大时，我们可以将发生的频率作为事件发生的概率的近似值，即 　　　　　　　　　　　　.

1.随机事件的概率：

我们已经学习用概率表示一个事件在一次试验或观测中发生的可能性的大小，它是在-之间的一个数，将这个事件记为，用表示事件发生的概率.怎样确定某一事件发生的概率呢？

实验1

奥地利遗传学家(G.Mendel)用豌豆进行杂交试验，下表为试验结果(其中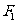为第一子代，为第二子代)：

性状	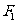的表现	的表现
种子的形状	全部圆粒	圆粒5474	皱粒1850	圆粒︰皱粒≈2.96︰1
茎的高度	全部高茎	高茎787	矮茎277	高茎︰矮茎≈2.84︰1
子叶的颜色	全部黄色	黄色6022	绿色2001	黄色︰绿色≈3.01︰1
豆荚的形状	全部饱满	饱满882	不饱满299	饱满︰不饱满≈2.95︰1

孟德尔发现第一子代对于一种性状为必然事件，其可能性为100%,另一种性状的可能性为0，而第二子代对于前一种性状的可能性约为75%,后一种性状的可能性约为25%，通过进一步研究，他发现了生物遗传的基本规律.

实际上，孟德尔是从某种性状发生的频率作出估计的.

实验2

　 在《算法初步》一章中，我们曾设计了一个抛掷硬币的模拟试验.下表是连续8次模拟试验的结果：

我们看到，当模拟次数很大时，正面向上的频率值接近于常数0.5，并在其附近摆动.

实验3

的前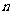位小数中数字6出现的频率

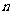	数字6出现的次数	数字6出现的频率
100	9	0.090000
200	16	0.080000
500	48	0.096000
1000	94	0.094000
2000	200	0.100000
5000	512	0.102400
10000	1004	0.100400
50000	5017	0.100340
1000000	99548	0.099548

从上表可以看出：数字6在的各位小数数字中出现的频率接近常数0.1，并在其附近摆动。如果统计0至9这10个数字在的各位小数数字中出现的频率值，可以发现它们都是接近常数0.1，并在其附近摆动.

[总结]在相同条件下，随着试验次数的增多，随机事件发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画该随机事件发生的可能性大小，而将频率作为其近似值。

2．通过对概率的学习，使学生对对立统一的辨证规律有进一步的认识.

[课堂互动]

自学评价

1.理解随机事件的频率定义及概率的统计定义，知道根据概率的统计定义计算概率的方法, 理解频率和概率的区别和联系；