1.概率： 一般地，如果随机事件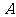在次试验中发生了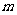次，当试验的次数很大时，我们可以将发生的频率作为事件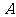发生的概率的近似值，即

1.随机事件的概率：

我们已经学习用概率表示一个事件在一次试验或观测中发生的可能性的大小，它是在-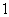之间的一个数，将这个事件记为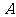，用表示事件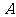发生的概率.怎样确定某一事件发生的概率呢？

实验1

奥地利遗传学家(G.Mendel)用豌豆进行杂交试验，下表为试验结果(其中为第一子代，为第二子代)：

性状	的表现	的表现
种子的形状	全部圆粒	圆粒5474	皱粒1850	圆粒︰皱粒≈2.96︰1
茎的高度	全部高茎	高茎787	矮茎277	高茎︰矮茎≈2.84︰1
子叶的颜色	全部黄色	黄色6022	绿色2001	黄色︰绿色≈3.01︰1
豆荚的形状	全部饱满	饱满882	不饱满299	饱满︰不饱满≈2.95︰1

孟德尔发现第一子代对于一种性状为必然事件，其可能性为100%,另一种性状的可能性为0，而第二子代对于前一种性状的可能性约为75%,后一种性状的可能性约为25%，通过进一步研究，他发现了生物遗传的基本规律.

实际上，孟德尔是从某种性状发生的频率作出估计的.

实验2

　 在《算法初步》一章中，我们曾设计了一个抛掷硬币的模拟试验.下表是连续8次模拟试验的结果：

我们看到，当模拟次数很大时，正面向上的频率值接近于常数0.5，并在其附近摆动.

实验3

的前位小数中数字6出现的频率

	数字6出现的次数	数字6出现的频率
100	9	0.090000
200	16	0.080000
500	48	0.096000
1000	94	0.094000
2000	200	0.100000
5000	512	0.102400
10000	1004	0.100400
50000	5017	0.100340
1000000	99548	0.099548

从表3-1-2可以看出：数字6在的各位小数数字中出现的频率接近常数0.1，并在其附近摆动。如果统计0至9这10个数字在的各位小数数字中出现的频率值，可以发现它们都是接近常数0.1，并在其附近摆动.

[总结]在相同条件下，随着试验次数的增多，随机事件发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画该随机事件发生的可能性大小，而将频率作为其近似值。

2．通过对概率的学习，使学生对对立统一的辨证规律有进一步的认识.

[课堂互动]

自学评价

1.理解随机事件的频率定义及概率的统计定义，知道根据概率的统计定义计算概率的方法, 理解频率和概率的区别和联系；

4.事件”某人掷骰子5次,两次点数为2”是随机事件吗?条件和结果是什么?一次试验是指什么?一共做了几次试验?

解: 是随机事件.条件:某人掷骰子5次,结果:两次点数为2,掷骰子一次就是一次试验,一共做了5次试验.

3.传说古时候有一个农夫正在田间干活,忽然发现一只兔子撞死在地头的木桩上,他喜出望外,于是拾起兔子回家了,第二天他就蹲在木桩旁守侯,就这样日复一日,年复一年,但再也没有等着被木桩碰死的兔子,这是为什么?

解:兔子碰死在木桩上是随机事件,可能不发生

2.下列试验中可以构成事件的是　　　　　　　　　　　　　　　　　　　 (　 D　 )

A、掷一次硬币

B、射击一次　

C、标准大气压下，水烧至100 ⁰C　　　

D、摸彩标中头奖

1.下列事件中随机事件的个数为　　　　　　　　　　　　　　　　　 　(　 B　 )

(1) 物体在重力作用下自由下落。

(2) 方程有两个不相等的实根

(3) 下周日下雨

(4) 某剧院明天的上座率不低于60%

A、1　　 B、2　 　C、3　　　 D、4

3、必然会发生的事件叫做必然事件；肯定不会发生的事件叫做不可能事件；在一定条件下，可能发生，也可能不发生的事件，叫做随机事件

[精典范例]

例1 观察下列现象：

(1)在标准大气压下水加热到100⁰C，沸腾；

(2)导体通电，发热；

(3)同性电荷，相互吸引；

(4)实心铁块丢人水中，铁块浮起；

(5)买一张福利彩票，中奖；

(6)掷一枚硬币，正面朝上；

其中是随机现象的有　　　　　　　　　

[解]显然(5)、(6)是随机现象。

注：显然(1)、(2)是必定发生的，、(3)、(4)是不可能发生的，从而它们都是确定性现象。

例2　 判断下列事件哪些是必然事件，哪些是不可能事件，哪些是随机事件？

(1)抛掷一块石子，下落；.

(2)在标准大气压下且温度低于0℃时，冰

融化；

(3)某人射击一次，中靶；

(4)如果，那么；

(5)掷两枚硬币，均出现反面；

(6)抛掷两枚骰子，点数之和为15；

(7)从分别标有号数1，2，3，4，5的5张

标签中任取一张，得到4号签；

(8)某电话机在1分钟内收到2次呼叫；

(9)绿叶植物，不会光合作用；

(10)在常温下，焊锡熔化；

(11)若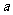为实数，则；

(12)某人开车通过十个路口，都遇到绿灯；

其中必然事件有　　　　　 ；不可能事件有　　　　　 ；随机事件有　　　　　

[解]根据定义，其中必然事件有(1)、(4)、(11)，不可能事件有(2)、(9)、(10)，随机事件有(3)、(5)、(6)、(7)、(8)、(12)

例3 在10个学生中,男生有个,现从10个学生中任选6人去参加某项活动.①至少有一个女生;②5个男生,1个女生;③3个男生,3个女生.当为何值时,使得①为必然事件,②为不可能事件,③为随机事件?

[解] “至少有1个女生”为必然事件，则有;

　 “5个男生,1个女生”为不可能事件，则有或;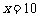

“3个男生,3个女生”为随机事件，则有;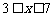

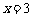综上所述,又由，可知或.

例4 已知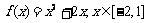,给出事件.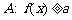

　(1)当A为必然事件时,求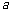的取值范围;

　(2)当A为不可能事件时,求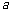的取值范围.

[解]

此时,

　 又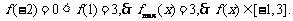

(1)当A为必然事件时,即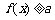恒成立,所以有,

则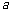的取值范围是

(2)当A为不可能事件时,即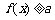一定不成立,

所以有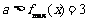,则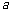的取值范围是

追踪训练

2、在一定条件下，某种现象可能发生，也可能不发生，事先不能断定出现哪种结果，这种现象叫做随机现象