
2.与几何概型有关的实际问题:长度问题、面积问题、体积问题、等候问题、约会问题、点集问题等等。
[精典范例]
例1 在1升高产小麦种子中混入了一种带麦诱病的种子,从中随机取出10毫升,则取出的种子中含有麦诱病的种子的概率是多少?
[分析]病种子在这1升中的分布可以看作是随机的,取得的10毫克种子可视作构成事件的区域,1升种子可视作试验的所有结果构成的区域,可用“体积比”公式计算其概率.
[解]取出10毫升种子,其中“含有病种子”这一事件记为A,则

答:所求概率为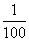 .
.
例2 如图, ,
,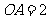 ,
, ,在线段
,在线段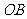 上任取一点
上任取一点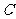 ,
,
试求:(1)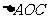 为钝角三角形的概率;
为钝角三角形的概率;
(2)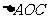 为锐角三角形的概率.
为锐角三角形的概率.
[解]如图,由平面几何知识:
当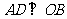 时,
时,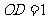 ;
;
当 时,
时,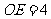 ,
,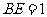 .
.
(1)当且仅当点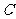 在线段
在线段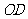 或
或 上时,
上时,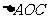 为钝角三角形
为钝角三角形
记"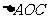 为钝角三角形"为事件
为钝角三角形"为事件 ,则
,则
即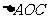 为钝角三角形的概率为
为钝角三角形的概率为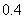 .
.
(2)当且仅当点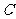 在线段
在线段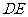 上时,
上时,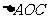 为锐角三角,
为锐角三角,
记"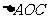 为锐角三角"为事件
为锐角三角"为事件 ,则
,则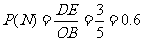
即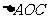 为锐角三角形的概率为
为锐角三角形的概率为 .
.
例3 一只蚂蚁在一边长为6的正方形区域内随机地爬行,求其恰在离四个顶点距离都大于3的地方的概率.
[解]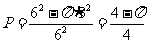
例4 利用随机模拟方法计算曲线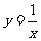 ,
,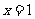 ,
,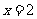 和
和 所围成的图形的面积.
所围成的图形的面积.
[分析]在直角坐标系中画出正方形(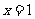 ,
,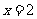 ,
, ,
,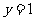 所围成的部分),用随机模拟的方法可以得到它的面积的近似值.
所围成的部分),用随机模拟的方法可以得到它的面积的近似值.
[解](1)利用计算器或计算机产生两组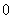 到
到 区间上的随机数,
区间上的随机数,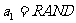 ,
,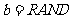 ;
;
(2)进行平移变换: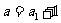 ;(其中
;(其中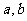 分别为随机点的横坐标和纵坐标)
分别为随机点的横坐标和纵坐标)
(3)数出落在阴影内的点数 ,用几何概型公式计算阴影部分的面积.
,用几何概型公式计算阴影部分的面积.
例如,做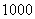 次试验,即
次试验,即 ,模拟得到
,模拟得到 ,
,
所以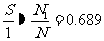 ,即
,即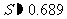 .
.
[说明]模拟计算的步骤:
(1)构造图形(作图);
(2)模拟投点,计算落在阴影部分的点的频率 ;
;
(3)利用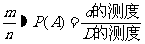 算出相应的量.
算出相应的量.
追踪训练
1.几何概型的概率:
一般地,在几何区域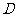 中随机地取一点,记事件"该点落在其内部一个区域
中随机地取一点,记事件"该点落在其内部一个区域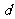 内"为事件
内"为事件 ,则事件
,则事件 发生的概率
发生的概率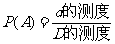 .
.
2、将实际问题转化为几何概型,并正确应用几何概型的概率计算公式解决问题.
[课堂互动]
自学评价
1、增强几何概型在解决实际问题中的应用意识.
3、某人午觉醒来,发现表停了,他打开收音机,想听电台的整点报时,求他等待的时间不多于15分钟的概率.
解:由几何概型的求概率的公式得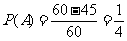 ,即“等待整点报时的时间不超过15分钟”的概率为
,即“等待整点报时的时间不超过15分钟”的概率为 .
.
2、在区间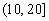 内的所有实数中,随机取一个实数
内的所有实数中,随机取一个实数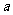 ,则这个实数
,则这个实数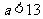 的概率是___
的概率是___ __.
__.
1、已知地铁列车每10min一班,在车站停1min,求乘客到达站台立即乘上车的概率.
解:由几何概型知,所求事件A的概率为:
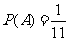 .
.
2、熟练运用几何概型解决关于时间类型问题.
[课堂互动]
自学评价
例1 在等腰直角三角形 中,在斜边
中,在斜边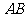 上任取一点
上任取一点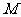 ,求
,求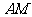 小于
小于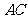 的概率.("测度"为长度)
的概率.("测度"为长度)

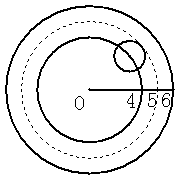 [分析]点
[分析]点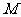 随机地落在线段
随机地落在线段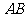 上,故线段
上,故线段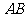 为区域
为区域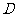 .当点
.当点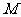 位于图
位于图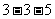 中线段
中线段 内时,
内时,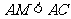 ,故线段
,故线段 即为区域
即为区域 .
.
[解]在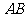 上截取
上截取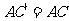 .于是
.于是
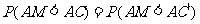
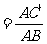

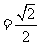 .
.
答: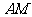 小于
小于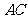 的概率为
的概率为 .
.
例2 某人欲从某车站乘车出差,已知该站发往各站的客车均每小时一班,求此人等车时间不多于10分钟的概率.
[分析]假设他在0-60分钟之间任何一个时刻到车站等车是等可能的,但在0到60分钟之间有无穷多个时刻,不能用古典概型公式计算随机事件发生的概率.可以通过几何概型的求概率公式得到事件发生的概率.因为客车每小时一班,他在0到60分钟之间任何一个时刻到站等车是等可能的,所以他在哪个时间段到站等车的概率只与该时间段的长度有关,而与该时间段的位置无关,这符合几何概型的条件.
[解]设A={等待的时间不多于10分钟},我们所关心的事件A恰好是到站等车的时刻位于[50,60]这一时间段内,因此由几何概型的概率公式,得P(A)= 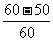 =
= ,即此人等车时间不多于10分钟的概率为
,即此人等车时间不多于10分钟的概率为 .
.
[说明]在本例中,到站等车的时刻X是随机的,可以是0到60之间的任何一刻,并且是等可能的,我们称X服从[0,60]上的均匀分布,X为[0,60]上的均匀随机数.
[小结]在许多实际问题中,其几何概型特征并不明显,要能将它们转化为几何概型,并正确应用几何概型的概率计算公式解决问题.如与时间有关的等候问题、约会问题,与数域有关的点集问题等等。
[精典范例]
例3 有一个半径为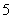 的圆,现在将一枚半径为
的圆,现在将一枚半径为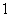 硬币向圆投去,如果不考虑硬币完全落在圆外的情况,试求硬币完全落入圆内的概率.
硬币向圆投去,如果不考虑硬币完全落在圆外的情况,试求硬币完全落入圆内的概率.
[解]由题意,如图,因为硬币完全落在圆外的情况是不考虑的,所以硬币的中心均匀地分布在半径为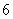 的圆
的圆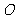 内,且只有中心落入与圆
内,且只有中心落入与圆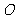 同心且半径为
同心且半径为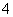 的圆内时,硬币才完全落如圆内.记"硬币完全落入圆内"为事件
的圆内时,硬币才完全落如圆内.记"硬币完全落入圆内"为事件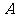 ,则
,则 .
.
答:硬币完全落入圆内的概率为 .
.
例4 约会问题
两人相约8点到9点在某地会面,先到者等候另一人20分钟,过时就可离去,试求这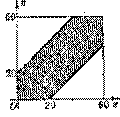 两人能会面的概率.
两人能会面的概率.
[解]以 分别表示两人的到达时刻,则两人能会面的充要条件为
分别表示两人的到达时刻,则两人能会面的充要条件为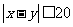 ,这是一个几何概率问题,可能的结果全体是边长为60的正方形里的点,能会面的点的区域用阴影标出(如上图).所求概率为
,这是一个几何概率问题,可能的结果全体是边长为60的正方形里的点,能会面的点的区域用阴影标出(如上图).所求概率为
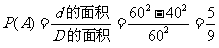 .
.
答:两人会面的概率为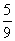 .
.
追踪训练
1、能运用模拟的方法估计概率,掌握模拟估计面积的思想;
3、靶子由三个半径分别为R,2R,3R的同心圆组成,如果你向靶子随机地掷一个飞镖,命中半径分别为R区域,2R区域,3R区域的概率分别为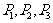 ,则
,则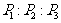 =____
=____ __.
__.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com