
2.(本小题满分15分)已知 ,
, (
( )是实数,方程
)是实数,方程 有两个实根
有两个实根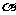 ,
, ,数列
,数列 满足
满足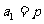 ,
,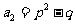 ,
,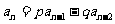 (
( 3,4,…).
3,4,…).
(I)求数列 的通项公式(用
的通项公式(用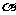 ,
, 表示);
表示);
(II)若 ,
,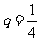 ,求
,求 的前
的前 项和.
项和.
1.(本小题满分14分)设直线 :
: (其中
(其中 ,
, 为整数)与椭圆
为整数)与椭圆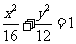 交于不同两点
交于不同两点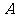 ,
, ,与双曲线
,与双曲线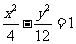 交于不同两点
交于不同两点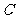 ,
,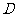 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量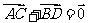 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
8.某车站每天8∶00-9∶00,9∶00-10∶00都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为
|
到站时刻 |
8∶10 9∶10 |
8∶30 9∶30 |
8∶50 9∶50 |
|
概率 |
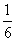 |
 |
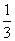 |
一旅客8∶20到车站,则它候车时间的数学期望为 (精确到分).
7.一个由若干行数字组成的数表,从第二行起每一行中的数字均等于其肩上的两个数之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是
(可以用指数表示).
6.若方程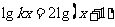 仅有一个实根,那么
仅有一个实根,那么 的取值范围是
.
的取值范围是
.
5.椭圆 (
( )上任意两点
)上任意两点 ,
,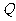 ,若
,若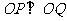 ,则乘积
,则乘积 的最小值为
.
的最小值为
.
4.使不等式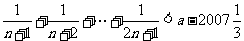 对一切正整数
对一切正整数 都成立的最小正整数
都成立的最小正整数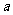 的值为
.
的值为
.
3.在坐标平面上有两个区域 和
和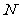 ,
, 为:
为:
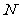 是随
是随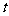 变化的区域,它由不等式
变化的区域,它由不等式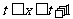 所确定,
所确定,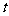 的取值范围是
的取值范围是 ,设
,设 和
和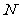 的公共面积是函数
的公共面积是函数 ,则
,则 .
.
2.已知直线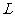 :
: 和圆
和圆 :
: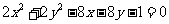 ,点
,点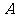 在直线
在直线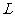 上,
上, 、
、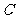 为圆
为圆 上两点,在△
上两点,在△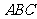 中,
中,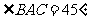 ,
, 过圆心
过圆心 ,则点
,则点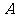 横坐标范围为
.
横坐标范围为
.
1.若函数 ,且
,且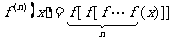 ,则
,则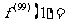 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com