
1.重点:双曲线的几何性质及初步运用.
(解决办法:引导学生类比椭圆的几何性质得出,至于渐近线引导学生证明.)
(三)学科渗透点
使学生进一步掌握利用方程研究曲线性质的基本方法,加深对直角坐标系中曲线与方程的关系概念的理解,这样才能解决双曲线中的弦、最值等问题.
(二)能力训练点
在与椭圆的性质的类比中获得双曲线的性质,从而培养学生分析、归纳、推理等能力.
(一)知识教学点
使学生理解并掌握双曲线的几何性质,并能从双曲线的标准方程出发,推导出这些性质,并能具体估计双曲线的形状特征.
13.在 中,若
中,若 ,试判断
,试判断 的形状。
的形状。
12. △ABC中,a、b、c分别是角A、B、C的对边,
 (1)求B的大小;(2)若b=
(1)求B的大小;(2)若b=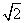 ,求a+c的最大值.
,求a+c的最大值.
11.已知A、B、C的坐标分别为A , B
, B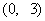 , C
, C ,
,  .
.
(1) 若
 , 求角
, 求角 的值; (2) 若
的值; (2) 若 , 求
, 求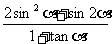 的值.
的值.
10.若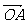 =a,
=a, =b,则∠AOB平分线上的向量
=b,则∠AOB平分线上的向量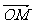 为
为
A. B.
B. (
( ),
), 由
由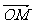 决定 C.
决定 C. D.
D.
9.设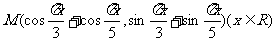 为坐标平面内一点,O为坐标原点,记f(x)=|OM|,当x变化时,函数 f(x)的最小正周期是 ( )
为坐标平面内一点,O为坐标原点,记f(x)=|OM|,当x变化时,函数 f(x)的最小正周期是 ( )
A.30π B.15π C.30 D.15
8.已知i , j为互相垂直的单位向量, 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com