还有诸如“均值换元”“设差换元”的方法，有兴趣的课后还可进一步学习。

例六：证明：若a > 0，则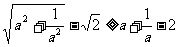

　 证：设

则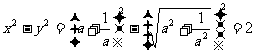

　( 当a = 1时取“=” )

∴

即　　 ∴原式成立

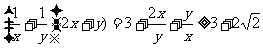证一： 即：

证二：由x > 0 , y > 0，2x + y = 1，可设

　　　 则

例三：若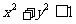，求证：

　 证：设，

　　　 则

例四：若x > 1，y > 1，求证：

　 证：设

　　　 则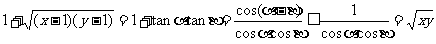

例五：已知：a > 1, b > 0 , a - b = 1，求证：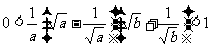

　 证：∵a > 1, b > 0 , a - b = 1　 ∴不妨设

　　 　则

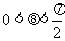　　 ∵,　 ∴0 < sinq < 1　　 ∴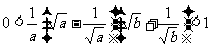

小结：若0≤x≤1，则可令x = sinq ()或x = sin²q ()。

若，则可令x = cosq , y = sinq ()。

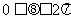若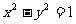，则可令x = secq, y = tanq ()。

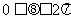若x≥1，则可令x = secq ()。

若xÎR，则可令x = tanq ()。

证一：(综合法)

∵

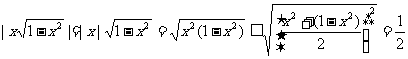
即：　 ∴

证二：(换元法) ∵　 ∴令 x = cosq ,　 qÎ[0, p]

则

∵　　 ∴

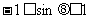第一节：基础写作：(共1小题，满分15分)

根据以下内容写一篇说明文，标题为“Australia”。

　1)、澳大利亚位于太平洋的西侧，是大洋洲(Oceania)最大的国家，面积760万平方公里。

2)、人口稀少，只有1，000多万，多数集中在东部沿海地区。

3)、首都堪培拉(Canberra)风景秀丽。

4)、悉尼(Sydney)是澳大利亚最大城市。有许多名胜，其中悉尼歌剧院(Opera House)闻名于世。2000年奥运会就是在悉尼举行的。

[写作要求]

　　　 1. 只能使用5个句子表达全部的内容。

　　　 2. 可以根据内容要点适当增加细节，但不要逐字翻译。