
2.函数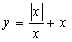 的图象是( )
的图象是( )

1.函数 的定义域为(
)
的定义域为(
)
A.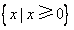 B.
B.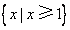 C.
C. D.
D.
知识体系············································································88
题型体系············································································93
题型一 导数的运算···································································94
题型二 复合函数求导(理科)··························································95
题型三 导数的几何意义·······························································98
题型四 利用导数判断函数单调性·······················································101
题型五 利用导数求函数的极值·························································105
题型六 利用导数求解或证明不等式·····················································107
答案部分················································································109
知识体系 三角函数部分······························································37
题型体系 三角函数部分······························································45
题型一 三角函数的概念······························································45
题型二 同角三角函数的关系与诱导公式················································49
题型三 两角和与差、二倍角公式······················································54
题型四 三角函数的图像······························································59
题型五 三角函数的性质(一) 定义域、值域、周期··········································· 65
题型六 三角函数的性质(二) 偶性性、单调性············································70
知识体系 解三角形部分·······························································77
题型体系 解三角形部分······························································77
题型一 解三角形····································································79
题型二 解三角形综合································································81
题型三 解三角形应用································································83
题型一 映射与函数的基本概念······················································1
题型二 定义域与值域······························································6
题型三 解析式的求解································································11
题型四 函数的性质(一) 奇偶性························································· 14
题型五 函数的性质(二) 单调性与最值················································19
题型六 指对幂函数运算法则及其图像··················································23
题型七 函数的图像与变换····························································26
题型八 函数的应用··································································33
10.福建省龙岩二中2010届高三摸底考试如图所示在工厂的流水线上安装的足够长的水平传送带。用水平传送带传送工件,可大大提高工作效率,水平传送带以恒定的速度v=2m/s运送质量为m=0.5kg的工件。工件都是以v0=1m/s的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数 ,每当前一个工件在传送带上停止相对滑动时,后一个工件立即滑上传送带。取g=10m/s2,求:
,每当前一个工件在传送带上停止相对滑动时,后一个工件立即滑上传送带。取g=10m/s2,求:
(1)工件经多长时间停止相对滑动
 (2)在正常运行状态下传送带上相邻工件间的距离
(2)在正常运行状态下传送带上相邻工件间的距离
(3)摩擦力对每个工件做的功
(4)每个工件与传送带之间的摩擦产生的内能
解:(1)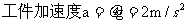


(2)
 ,则两物相距
,则两物相距 (也可直接
(也可直接 )
)
(3)
(4)
9.安徽省两地2010届高三第一次联考检测如图所示,一个质量为m的圆环套在一根固定的水平直杆上,环与杆的动摩擦因数为μ,现给环一个向右的速度v0,如果环在运动过程中还受到一个方向始终竖直向上的力F的作用,已知F=kv(k为常数,v为速度),求环在运动过程中克服摩擦力所做的功(假设杆足够长)。

解:当mg=kv0时,即v0= 时,环作匀速运动,Wf=0,环克服摩擦力所做的功为零;(3分)
时,环作匀速运动,Wf=0,环克服摩擦力所做的功为零;(3分)
当mg>kv0时,即v0< 时,环在运动过程中,v减少,F减少,f增大,最终环静止Wf=
时,环在运动过程中,v减少,F减少,f增大,最终环静止Wf=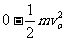 ,环克服摩擦力所做的功为
,环克服摩擦力所做的功为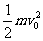 。
(5分)
。
(5分)
当mg<kv0时,即v0> 时,环在运动过程中,v减少,F减少,f减少
时,环在运动过程中,v减少,F减少,f减少
到mg=kv时,环作匀速运动,Wf=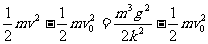 ,
,
环克服摩擦力所做的功为 ;
(7分)
;
(7分)
8. 湖北省众望高中2010届高三周练如图所示,长度为L的轻杆上端连着一质量为m的体积可忽略的小重物B.杆的下端用铰链固接于水平面上的A点.同时,置于同一水平面上的立方体C恰与B接触,立方体C的质量为M.今做微小的扰动,使杆向右倾倒,设B与C、C与水平面间均无摩擦,而B与C刚脱离接触的瞬间,杆与地面夹角恰好为π/6.求B与C的质量之比m/M。
湖北省众望高中2010届高三周练如图所示,长度为L的轻杆上端连着一质量为m的体积可忽略的小重物B.杆的下端用铰链固接于水平面上的A点.同时,置于同一水平面上的立方体C恰与B接触,立方体C的质量为M.今做微小的扰动,使杆向右倾倒,设B与C、C与水平面间均无摩擦,而B与C刚脱离接触的瞬间,杆与地面夹角恰好为π/6.求B与C的质量之比m/M。
解:根据题意,当B与C刚脱离接触的瞬间,C的水平速度达到最大,水平方向的加速度
为零,即水平方向的合外力为零.由于小球此时仅受重力和杆子作用力,而重力是竖直向下的,
所以杆子的作用力必为零.列以下方程:
mgsinθ=mv2/L,(3分)
vx=vsinθ,(2分)
vc=vx,(1分)
mgL(1-sinθ)=mv2/2+Mvc2/2(1分)
解以上各式得m/M=1/4(4分)
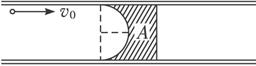
7.福建省龙岩二中2010届高三摸底考试如下图所示是固定在水平地面上的横截面为“ ”形的光滑长直导轨槽,槽口向上(图为俯视图)。槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“
”形的光滑长直导轨槽,槽口向上(图为俯视图)。槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“ ”形槽的宽度略小。现有半径r(r<<R)的金属小球以水平初速度V0冲向滑块,从滑块的一侧半圆形槽口边缘进入。已知金属小球的质量为m,木质滑块的质量为3m,整个运动过程中无机械能损失。求:
”形槽的宽度略小。现有半径r(r<<R)的金属小球以水平初速度V0冲向滑块,从滑块的一侧半圆形槽口边缘进入。已知金属小球的质量为m,木质滑块的质量为3m,整个运动过程中无机械能损失。求:
(1)当金属小球滑离木质滑块时,金属小球和木质滑块的速度各是多大;
(2)当金属小球经过木质滑块上的半圆柱形槽的最右端A点时,金属小球的对地速度。
解:(1)设滑离时小球喝滑块的速度分别为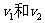 ,由动量守恒
,由动量守恒
又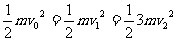
得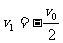

(2)小球过A点时沿轨道方向两者有共同速度v,沿切向方向速度为

 得
得

6. 江苏省淮阴中学2010届高三摸底考试质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞,碰后m2被右侧的墙原速弹回,又与m1相碰,碰后两球都静止。求:两球第一次碰后m1球的速度大小。
江苏省淮阴中学2010届高三摸底考试质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞,碰后m2被右侧的墙原速弹回,又与m1相碰,碰后两球都静止。求:两球第一次碰后m1球的速度大小。
解:根据动量守恒定律得: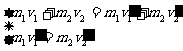 (2分)
(2分)
解得: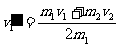 (2分)
(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com