
一)常见净化原理:气体的净化可分为物理方法和化学方法。遵循以下原理:
①不损失主体气体;②不引入新杂质;③在密闭容器中进行;④先除易除的气体。
1、物理方法:
(1)液化法:利用沸点不同从空气中分离N2和O2。
(2)水洗法:利用溶解度不同从N2和NH3中除去NH3;从NO和NO2中除去NO2。
|
(1)氧化还原法:灼热铜丝网除去混合物中的O2(2Cu+O2=2CuO);CuO除去H2、CO等。
(2)酸碱法:NH3和CO2通过碱石灰除去CO2。(CaO+CO2=CaCO3)
(3)沉淀法:除去CO2中的H2S通过CuSO4溶液。H2S+CuSO4=CuS↓+H2SO4
(4)最常用的为洗气法:
①用饱和NaCl除去Cl2中的HCl;
②用饱和NaHCO3除去CO2中的HCl、SO2等;
③用酸性高锰酸钾除去气体中的SO2;(如CO2中的SO2)
注意:以下考得比较少:
④用饱和NaHSO3除去SO2中的SO3;[浓硫酸也可除SO3(SO3易溶于浓硫酸)];冷却同样可以除SO3。
⑤用饱和Na2CO3溶液除去乙酸乙酯中的乙醇或乙酸;
三)固+液或液+液(加热):适用于制C2H4、Cl2、SO2、乙酸乙酯、蒸馏(HCl课本没有)






a b c d e f

注意点:
1、用KMnO4制取O2时,为了防止生成的细小颗粒堵塞导管,在大试管口放一松软棉花。
2、实验室制取氨气时,由于氨气极易与空气中的水结合,导致外部空气向试管里“冲”,里面氨气向外逸出,在小试管口放一疏松棉花。
3、在制取C2H2时,若用大试管为反应器时,在大试管口放一松软棉花,防止生成的泡沫喷出。
4、Cu和浓硫酸制取SO2做性质试验的小试管口堵一块蘸有少量碱液的棉花防止污染。
(二)启普发生器类
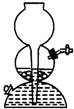
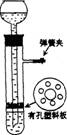
二)固+液体(不加热):适用于制CO2、H2 、H2S(SO2、NO2、NO课本没有制法)
|
|



一)固+固(加热):适用于制O2、NH3、(CH4课本没有)
|

10.(08枣庄)如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=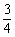 .
.
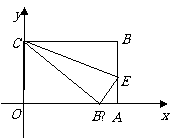 (1)求B′点的坐标;
(1)求B′点的坐标;
(2)求折痕CE所在直线的解析式.
9. 反比例函数y= 的图象在第一象限的分支上有一点A(3,4),P为x轴正半轴上的一个动点,
的图象在第一象限的分支上有一点A(3,4),P为x轴正半轴上的一个动点,
(1)求反比例函数解析式.
(2)当P在什么位置时,△OPA为直角三角形,求出此时P点的坐标.
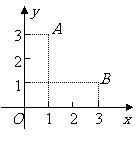
8. 已知点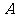 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为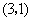 .
.
⑴ 写出一个图象经过 两点的函数表达式;
两点的函数表达式;
⑵ 指出该函数的两个性质.
21. (本小题满分14分)
解:(Ⅰ)设 ,则
,则
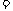

 ,所以
,所以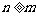 . 2分
. 2分
(Ⅱ) ,令
,令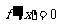 ,得
,得 .…………3分
.…………3分
当 时,
时,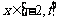 时,
时, ,
,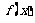 是递增函数;当
是递增函数;当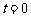 时,显然
时,显然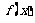 在
在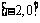 也是递增函数.…………4分
也是递增函数.…………4分
∵ 是
是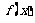 的一个极值点,∴当
的一个极值点,∴当 时,函数
时,函数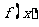 在
在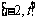 上不是单调函数.∴当
上不是单调函数.∴当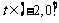 时,函数
时,函数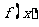 在
在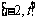 上是单调函数.……5分
上是单调函数.……5分
(Ⅲ)由(1),知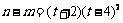 ,∴
,∴ .…………6分
.…………6分
又∵ , 我们只要证明方程
, 我们只要证明方程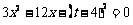 在
在 内有解即可.…………7分
内有解即可.…………7分
记 ,则
,则
 ,
, ,
,
 ,
,
∴ .…………9分
.…………9分
①当 时,
时,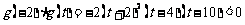 ,方程
,方程 在
在 内有且只有一解;…………10分
内有且只有一解;…………10分
②当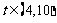 时,
时,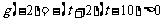 ,
, ,又
,又 ,∴方程
,∴方程 在
在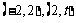 内分别各有一解,方程
内分别各有一解,方程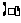 在
在 内两解;…………11分
内两解;…………11分
③当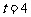 时,方程
时,方程 在
在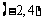 内有且只有一解
内有且只有一解 ;……12分
;……12分
④当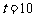 时,方程
时,方程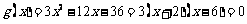 在
在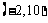 内有且只有一解
内有且只有一解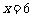 .…………13分
.…………13分
综上,对于任意的 ,总存在
,总存在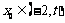 ,满足
,满足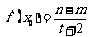 .
.
当 时,满足
时,满足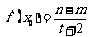 ,
,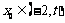 的
的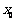 有且只有一个;
有且只有一个;
当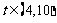 时,满足
时,满足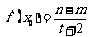 ,
,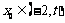 的
的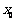 恰有两个.…………14分
恰有两个.…………14分
20.(本小题满分14分)
解:(Ⅰ) ∵ ,∴
,∴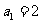 .
-------2分
.
-------2分
当 时,
时, ,
,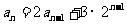 ,于是
,于是 ;-------4分
;-------4分
令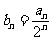 ,则数列
,则数列 是首项
是首项 、公差为
、公差为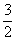 的等差数列,
的等差数列, ;
;
∴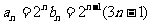 .
-------6分
.
-------6分
(Ⅱ) ∵ ,
,
∴ ,
-------8分
,
-------8分
记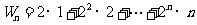 ①,则
①,则 ②,-------10分
②,-------10分
①-②有 ,
,
∴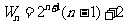 .
-------12分
.
-------12分
故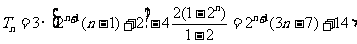 -------14分
-------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com