
2.(07湖北)如图,一次函数 的图象经过A、B两点,
的图象经过A、B两点,
则关于x的不等式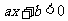 的解集是
.
的解集是
.
1. (07福建)若正比例函数
(07福建)若正比例函数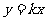 (
( ≠
≠ )经过点(
)经过点(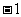 ,
,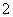 ),则该正比例函数的解析式为
),则该正比例函数的解析式为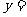 ___________.
___________.
21.[解析](Ⅰ) .
.
……………………………………………………………………………………………2分
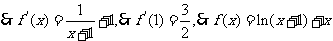 .……………………………4分
.……………………………4分
(Ⅱ) 时恒成立,即
时恒成立,即
 在
在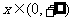 时恒成立,令
时恒成立,令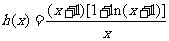 ,所以
,所以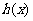 的最小值大于
的最小值大于 .……………………………………………………………………………………………6分
.……………………………………………………………………………………………6分
 ,
,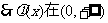 上单调递增.又
上单调递增.又 存在唯一实根
存在唯一实根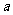 ,且满足
,且满足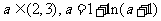 .………………………………………………………………………………10分
.………………………………………………………………………………10分
当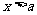 时,
时,
 ,所以k=3.………………………………………………………14分
,所以k=3.………………………………………………………14分
20.[解析](Ⅰ)设直线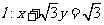 与椭圆
与椭圆 交于
交于 ,
,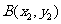 由
由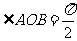 ,知
,知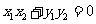 ,
………………………………………………………………2分
,
………………………………………………………………2分
而 代入上式得到
代入上式得到
 ; ……………………………………………………3分
; ……………………………………………………3分
而 知
知 ,即
,即 ;不妨设
;不妨设 则
则 ………………5分
………………5分
 .
.

 或
或 ,或
,或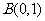 .
.
 不合题意,舍去.………………………………7分
不合题意,舍去.………………………………7分
 ,则椭圆方程为
,则椭圆方程为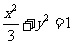 ,
,
故所求椭圆方程为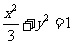 .……………………………………………………8分
.……………………………………………………8分
(Ⅱ)
 是椭圆
是椭圆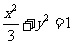 上的点,且
上的点,且 ,
,
故设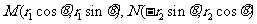 . ………………………… 10分
. ………………………… 10分
于是
 ,
,
从而 .…………………………………………………………12分
.…………………………………………………………12分
又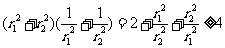 ,从而
,从而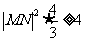 即
即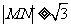 ,
,
故所求 的最小值为
的最小值为 .…………………………………………… 14分
.…………………………………………… 14分
19.[解析]解法1:(Ⅰ) ①证明: ∵平面ACEF⊥平面ABCD,EC⊥AC,
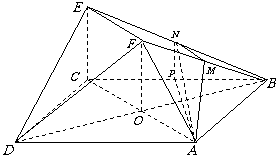 ∴EC⊥平面ABCD;连接BD交AC于点O,连接FO,
∴EC⊥平面ABCD;连接BD交AC于点O,连接FO,
∵正方形ABCD的边长为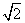 ,∴AC=BD=2;
,∴AC=BD=2;
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1;易求得DF=BF=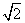 ,
,
DE=BE= ,由勾股定理知 DF⊥EF,BF⊥EF,
,由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角,
由BF=DF=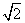 ,BD=2可知∠BFD=
,BD=2可知∠BFD= ,
,
∴平面BEF⊥平面DEF. ………………(7分)
(Ⅱ)取BF中点M,BE中点N,连接AM、MN、AN,∵AB=BF=AF=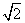 ,∴AM⊥BF,
,∴AM⊥BF,
又∵MN∥EF,EF⊥BF,∴MN⊥BF,∴∠AMN就是二面角A-BF-E的平面角.
易求得 ,
, ;
;
在Rt△ 中,可求得
中,可求得 ,
,
∴在△ 中,由余弦定理求得
中,由余弦定理求得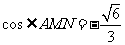 . ……………………………(13分)
. ……………………………(13分)
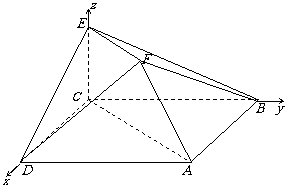 解法2:(Ⅰ)∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD;
解法2:(Ⅰ)∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD;
建立如图所示的空间直角坐标系C-xyz,则 ,
,
 ,
, ,
, ,
, ,
,
∴ ,
, ,
,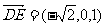 .…(2分)
.…(2分)
设平面BEF、平面DEF的法向量分别为
 ,则
,则
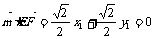 ①,
①,
 ②,
②, ③,
③, 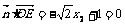 ④.
④.
由①③③④解得 ,∴
,∴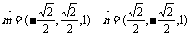 ,…(5分)
,…(5分)
∴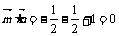 ,∴
,∴ ,故平面BEF⊥平面DEF.……………………………………(7分)
,故平面BEF⊥平面DEF.……………………………………(7分)
(Ⅱ)设平面ABF的法向量为 ,∵
,∵ ,
, ;
;
∴ ,
,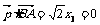 ,解得
,解得 .
.
∴ ,……………………………………………………………………………(9分)
,……………………………………………………………………………(9分)
∴ .………………………………………………(11分)
.………………………………………………(11分)
由图知,二面角A-BF-E的平面角是钝角,故所求二面角的余弦值为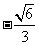 .…(13分)
.…(13分)
18. [解析](Ⅰ)由题意规律,编号为2的同学看到的像是(6,8);
编号为3的同学看到的像是(8,11).…………………………………………4分
(Ⅱ)设编号为 的同学看到的像是
的同学看到的像是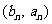 ,则
,则 ,
,
当 时,
时, .…………………………………………………………5分
.…………………………………………………………5分
由题意 , ∴
, ∴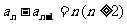 .…………………………6分
.…………………………6分
∴ =
= =
= .…10分
.…10分
 ,
, .………………12分
.………………12分
经检验 时,上式也成立.
时,上式也成立.
∴编号为 的同学看到的像是
的同学看到的像是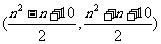 .………………………………13分
.………………………………13分
17.[解析](Ⅰ)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3. ……3分
(Ⅱ)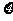 的可能值为8,10,12,14,16,
……4分
的可能值为8,10,12,14,16,
……4分
P(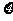 =8)=0.22=0.04, P(
=8)=0.22=0.04, P(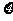 =10)=2×0.2×0.5=0.2,
……6分
=10)=2×0.2×0.5=0.2,
……6分
P(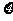 =12)=0.52+2×0.2×0.3=0.37,
=12)=0.52+2×0.2×0.3=0.37,
P(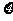 =14)=2×0.5×0.3=0.3,
=14)=2×0.5×0.3=0.3,
P(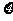 =16)=0.32=0.09. ……9分
=16)=0.32=0.09. ……9分
 |
8 |
10 |
12 |
14 |
16 |
|
P |
0.04 |
0.2 |
0.37 |
0.3 |
0.09 |
则 的分布列为
的分布列为
……11分 8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元). ……13分
16. [解析](Ⅰ)由 ,
,  ,
………………………2分
,
………………………2分
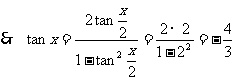 .
…………………5分
.
…………………5分
(Ⅱ) 原式= 

 …………………11
…………………11

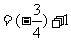
 .
…………………13
.
…………………13
(二)选做题(13-15题,考生只能从中选做两题)
13.(坐标系与参数方程选做题)[解析] .线的直角坐标方程为
.线的直角坐标方程为 ,极坐标方程为
,极坐标方程为 .
.
14.(不等式选讲选做题)[解析]5< <7.
<7. ,
,
∵解集中的整数有且仅有1,2,3,∴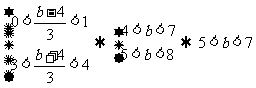 .
.
15.(几何证明选讲选做题) [解析].因为AC是圆
[解析].因为AC是圆 的切线,所以
的切线,所以 ,因为
,因为 是圆
是圆 的切线,所以
的切线,所以 ,
, .
.
(一)必做题(9-12题)
9. [解析]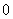 .
. ,
, .
.
10.[解析]
 系数为
系数为 .
.
11.[解析] .对应于
.对应于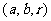 的圆
的圆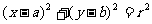 在第一象限,则掷的结果
在第一象限,则掷的结果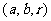 必须满足
必须满足 ,且
,且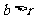 .其中,对应于
.其中,对应于 的有25个,对应于
的有25个,对应于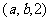 的有16个,对应于
的有16个,对应于 的有9个,对应于
的有9个,对应于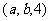 的有4个,对应于
的有4个,对应于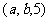 的有1个,所以概率是
的有1个,所以概率是 .
.
12.[解析]
 ,
,
 ,
, ),
), ,
,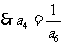
 ,故
,故 最大为
最大为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com