1、　 书本 P 85　 随堂练习　 1、2

2、　　 理解圆的概念和点与圆的位置关系

教学重点和难点

重点：点与圆的位置关系

难点：点与圆的位置关系

教学过程设计

一、　　　　 从学生原有的认知结构提出问题

与三角形、四边形一样，圆也是我们常见的图形。圆的半径、直径、周长、面积，我们并不陌生。在这一章里，我们将学习圆的更深入的知识。

二、　　　　 师生共同研究形成概念

1、 车轮为什么做成圆形

本节主要用集合的观点研究圆的概念及点与圆的位置关系。通过车轮的实例，让学生感受圆是生活中大量存在的图形。教学时，可以给学生展示正方形或长方形的车轮在行走时存在的问题，使学生感受圆形的车轮运转起来最平稳。从而使学生认识到圆上任意一点到圆心的距离是一个定值。

2、 圆的定义

☆　 议一议　　 书本P 83　 议一议

通过对游戏队形的讨论，使学生进一步认识圆的本质特征，为下面引出圆的定义做准备。如果单纯考虑队形因素，即只考虑“距离”对投圈结果的影响，那么排成圆形队形比较公平。学生在小学数学中已经学过圆的概念，书本在此用集合的观点给出了圆的描述性定义。

平面上到定点的距离等于定长的所有点组成的图形叫做圆；

其中，定点称为圆心；

定长称为半径的长。

“圆O”可表示成“⊙O”。

确定一个圆需要两个要素：一是圆心，二是半径。

3、 点与圆的位置关系

☆　 想一想　　 书本P 84　 想一想

通过投镖的情境引入点与圆的位置关系：点在圆上，点在圆外，点在圆内。

点O在圆外，即这个点到圆心的距离大于半径；

点O在圆上，即这个点到圆心的距离等于半径；

点O在圆内，即这个点到圆心的距离小于半径。

点与圆的位置关系可以转化为点到圆心的距离与半径之间的数量关系；反过来，也可以通过这种数量关系判断点与圆的位置关系。

☆　 做一做　　 书本P 85　 做一做

让学生再次经历用集合的观点理解图形的过程。

4、 讲解例题

例1　　　 《练习册》 P 43　 3

分析：通过题目已知的面积，间接得出圆的半径，再通过点与圆心的距离判断点是否在圆上。

三、　　　　 随堂练习

1、　　 经历形成圆的概念和点与圆的位置关系的过程

10. 如图，在边长为2的正方形ABCD的一边BC上，一点P从B点运动到C点，设BP＝x，四边形APCD的面积为y.

⑴ 写出y与x之间的函数关系式及x的取值范围；

⑵ 说明是否存在点P，使四边形APCD的面积为1.5？

9. 某地区的电力资源丰富，并且得到了较好的开发.该地区一家供电公司为了鼓励居民用电，采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图像如图所示.

⑴ 填空，月用电量为100度时，应交电费　　　　 元；

⑵ 当x≥100时，求y与x之间的函数关系式；

⑶ 月用电量为260度时，应交电费多少元？

8. 一次函数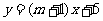中，的值随的增小而减小，则的取值范围是(　)

A．　　　 B． 　　 C．　　　 D．

7.(07浙江)一次函数与的图象

如图，则下列结论：①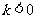；②；③当

时，中，正确的个数是(　　 )

A．0　　 　　 　　B．1　　 　C．2　 　　　 D．3

6. 直线与轴的交点是(1，0)，则的值是(　 　)

A.3　　　　　　 B.2　　　　　　 C.－2　　　　　　 D.－3

5. 下列各点中，在函数的图象上的是( 　　)

A．(2，3)　　 　B．(3，1)　　 　C．(0，－7)　　 　D．(－1，9)

4．(08上海)如图，将直线向上平移1个单位，得到一个

一次函数的图像，那么这个一次函数的解析式是　　　　 ．