
2.数列与函数相结合的考查
例2.已知数列 满足
满足 ,且
,且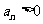 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 是否存在最大项?若存在最大项,求出该项和相应的项数;若不存在,说明理由.
是否存在最大项?若存在最大项,求出该项和相应的项数;若不存在,说明理由.
点拔:根据所给的条件, ,从方程的角度来思考,将
,从方程的角度来思考,将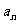 当成末知数,则可得到一个关于
当成末知数,则可得到一个关于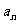 的一元二次方程,用求根公式可求得.第(2)问建立关于n的函数,再利用导数来判断函数的单调性,进而可求得最值.
的一元二次方程,用求根公式可求得.第(2)问建立关于n的函数,再利用导数来判断函数的单调性,进而可求得最值.
解析:(1)由 得
得
由一元二次方程求根公式得
∵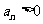 ∴
∴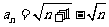
(2)由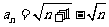 知数列
知数列 各项满足函数
各项满足函数
∵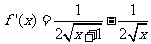 当
当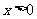 时,
时,
∴当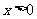 时
时 ,即函数
,即函数 在
在 上为减函数
上为减函数
即有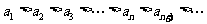 ∴数列
∴数列 有最大项,最大项为第一项
有最大项,最大项为第一项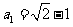 .
.
点评:本题第(1)问是用方程的思想看待等式 ,则可以用解方程来求解,通常在解等差数列、等比数列的问题时,常常将题设条件转化成关于
,则可以用解方程来求解,通常在解等差数列、等比数列的问题时,常常将题设条件转化成关于 和d(或q)的方程(组)通过求解方程(组)来解决问题.求数列中的最值问题一般是建立n的函数,但要注意n的取值为正自然数.
和d(或q)的方程(组)通过求解方程(组)来解决问题.求数列中的最值问题一般是建立n的函数,但要注意n的取值为正自然数.
1.数列本身的知识考查
例1.若等比数列 的前
的前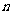 项和为
项和为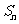 ,
,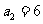 ,
,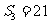 则公比
则公比 .
.
点拔:本题是等比数列中问题,常用的方法是以 和
和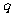 为未知数建立方程,解出
为未知数建立方程,解出 和
和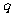
解析:2或 Þ q=2或
点评:数列中的填空题与选择题,常常是考查数列的概念、性质、通项公式等,解决问题的方法,基本上是转化为等差或等比数列,再用方程与数列性质来解决,即建立以 和
和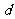 (或
(或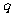 )为未知数建立方程,解出
)为未知数建立方程,解出 和
和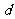 (或
(或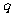 ),问题基本就可以解决了.
),问题基本就可以解决了.
数列是高中数学的得要内容,是高考的热点,也是进一步学习数学的基础,因此高考对这部分知识的考查的题型多样、解答题的难度也较高.纵观近几年的高考,关于数列的考查主要有以三个方面的内容:一是数列本身的知识,主要是等差数列、等比数列概念、通项公式、性质、前n项和公式;二是数列与其它知识的交汇如:与函数、方程、不等式、三角函数、解析几何等知识的结合;三是数列的应用问题,主要是增长率、分期付款等.试题主要体现中低档题为小题,数列与几何、函数、三角、不等式知识的结合为综合性高难度大的解答题.
5.注意在数列中的函数思想、方程的思想、分类讨论的思想方法在数列综合题中的应用.
4.数列求和的常用方法:通过数列的通项的构成可有拆项分组(适用数列的构成是由几个等差或等比数列的和或差);裂项相消(“裂”成某个数列的相邻两项的差,后叠加);错位相减(适用于一个等差数列的各项与等比数列的各项的相应乘积构成的数列).
3.在等差数列中,有关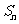 的最值问题的解决方法:一是用相邻项异号法求解;二是用
的最值问题的解决方法:一是用相邻项异号法求解;二是用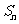 关于n的二次函数,由配方求得最值;特别要注意各项绝对值的数列的前n项和的最值,必须使用转化、化归的思想方法来解决.
关于n的二次函数,由配方求得最值;特别要注意各项绝对值的数列的前n项和的最值,必须使用转化、化归的思想方法来解决.
2.判断或者证明数列为等差数列(或等比数列)数列的四种常用方法:定义法、通项公式法、前n项和的公式法、等差(或等比)中项法.
1.等差、等比数列的概念、性质、通项公式及递推关系式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com