例4．已知集合P={-1,a,b}，Q={-1,a²,b²}，且Q=P，求1+a²+b²的值．

分析：含字母的两个集合相等，并不意味着 按序对应相等，要分类讨论，同时也要考虑集合中的元素的互异性和无序性.

追踪训练

1．集合A={x|y=x²+1}，B={t|p=t²+1}

　 C={y|x =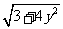}，这三个集合

　 的关系？

3. 下列集合表示法正确的是

　(1) {1，2，2}；

　(2) {Ф}；

　(3) {全体有理数}；

(4) 方程组的解的集合为

{2，4}；

(5)不等式x²-5>0的解集为{x²-5>0}.

例3．已知A={a|}，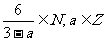

试用列举法表示集合A．

分析：用列举法表示的集合，要认清集合的实质，集合中的元素究竟满足哪

　些条件．

点评:本题实际上是要求满足6被3-a整除的

　　 整数a的值，若将题目改为，

　　 　则集合A={-3，0，1，2，4，5，6，9}.

2. 用描述法表示下列集合：

　(1) 奇数的集合；

　(2)正偶数的集合；

　(3)不等式2x-3>5的解集；

　(4)直角坐标平面内属于第四象限的点的

　　 集合；　　　　　　　　 　.

例1．用列举法表示下列集合：

(1)中国国旗的颜色的集合；

(2)单词mathematics中的字母的集合；

　(3)自然数中不大于10的质数的集合；　

(4)同时满足的整数解的

集合；

(5)由所确定的实数

　 集合.

(6){(x,y)|3x+2y=16，x∈N，y∈N }

分析：先求出集合的元素，再用列举法

　　　 表示.

点评:

(1)用列举法表示集合的步骤为：

　　 ①求出集合中的元素

　　 ②把这些元素写在花括号内

(2)用列举法表示集合的优点是元素一目了

　　 然；缺点是不易看出元素所具有的属性.

例2．用描述法表示下列集合：

　 (1)所有被3整除的整数的集合；

　 (2)使有意义的x的集合；

　 (3)方程x²+x+1=0所有实数解的集合；

　 (4)抛物线y=-x²+3x-6上所有点的集合；

　 (5)图中阴影部分内点的集合；

分析：用描述法表示来集合，先要弄清楚元素所具有的形式，从而写出其代表元素再确定元素所具有的属性即可.

点评: 用描述法表示集合时，注意确定和简

　　　 化集合的元素所具有的共同特性.

追踪训练一

1.用列举法表示下列集合：

　(1) {x|x²+x+1=0}

　(2){x|x为不大于15的正约数}

　(3) {x|x为不大于10的正偶数}

　(4){(x,y)|0≤x≤2，0≤y<2，x，y∈Z}

4． 由实数-x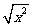，|x|，，x，组成的集合最多含有元素的个数

是_________________个

[选修延伸]

例6：设S是满足下列两个条件的实数所构成

　　 的集合：

　①1∈S，②若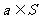，则，请

解答下列问题：

(1)若2∈S，则S中必有另外两个数，求

出这两个数；

(2)求证：若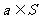，则

(3)在集合S中元素能否只有一个？请说明

　　 理由；

(4)求证：集合S中至少有三个不同的元素.

点评: (4)证明中需说明三个数互不相等，

　　　 否则证明欠严谨.数学是一门非常

严谨的科学.

[师生互动]

3．用∈或填空

　　　 1_______N　 -3_________N　　 0__________N　　 ________N

　　　 1_______Z -3_________Q　　 0__________Z　　 ________R

　　　 0_______N*　　 ________R　 _______Q　　　 cos30⁰_______Z

2．下列写法正确的是___________________

　 ①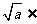Q　

　②当n∈N时，由所有(-1)ⁿ的数值组成的集合为无限集　

③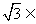R

　 ④-1∈Z ⑤由book中的字母组成的集合与元素k，o，b组成的集合是同一个集合

　　 把正确的序号填在横线上　　

些问题

例4：集合A中的元素由x=a+b(a∈Z,b

∈Z)组成，判断下列元素与集合A的

关系？

　　 (1)0　　　 (2)　　

　(3)

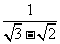
分析：先把x写成a+b的形式，再观察a，b是否为整数.

点评: 要判断某个元素是否是某个集合的元

素，就是看这个元素是否满足该集合

的特性或具体表达形式.

例5：不包含-1，0，1的实数集A满足条件a∈A，则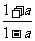∈A，如果2∈A,求A中的元素？

分析：该题的集合所满足的特征是由抽象的

　　　 语句给出的，把2这个具体的元素代入求出A的另一个元素，但该题要循环代入，求出其余的元素，同学们可能想不到.

追踪训练

1．下列研究的对象能否构成集合

　 ① 某校个子较高的同学；

　② 倒数等于本身的实数

③ 所有的无理数

　 ④ 讲台上的一盒白粉笔

　 ⑤中国的直辖市

⑥中国的大城市　

例1．下列研究的对象能否构成集合

　(1)世界上最高的山峰　　　

(2)高一数学课本中的难题

　(3)中国国旗的颜色　　　　

(4)充分小的负数的全体

　(5)book中的字母　　　　

(6)立方等于本身的实数

(7)不等式2x-8<13的正整数解

[解]

点评:判断一组对象能否组成集合关键是能否找到一个明确的标准，按照这个确定的标准，它要么是这个集合的元素，

要么不是这个集合的元素，即元素确

定性.

例2：集合M中的元素为1，x，x²-x，求x的范围？

分析：根据集合中的元素互异性可知：集合里的元素各不相同，联列不等式组.

点评: 元素的特性(特别是互异性)

是解决问题的切入点.

例3：三个元素的集合1，a，，也可表示

为0，a²，a+b，求a²⁰⁰⁵+ b²⁰⁰⁶的值．

分析：三个元素的集合也可表示另外一种形

式，说明这两个集合相同，而该题目

从特殊元素0入手，可以省去繁琐的讨论．

点评:从特殊元素入手，灵活运用集合的三

个特征．　　

6．集合的分类：

按它的元素个数多少来分：

(i) 　　　　_________________

叫做有限集；

(ii)________________________

叫做无限集；

(iii)　　　　 _______________

叫做空集，记为_____________

[精典范例]