
例4: 已知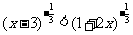 ,求
,求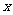 的取值范围.
的取值范围.
分析:数形给合思想的运用.由于不等式的左右两边的幂指数都是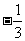 ,因此可借助于幂函数
,因此可借助于幂函数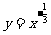 的图象性质来求解.
的图象性质来求解.
点评:利用函数图象特征了解函数的性质,利用函数性质去解不等式.
4.证明:函数 在
在 上是减函数.
上是减函数.
.
|
学生质疑 |
|
|
教师释疑 |
|
3.若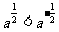 ,则
,则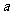 的取值范围是 ( )
的取值范围是 ( )
A.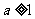 B.
B.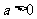 C.
C.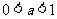 D.
D.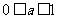
2.函数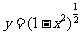 的值域是 ( )
的值域是 ( )
A. B.
B.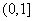 C.
C.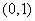 D.
D.
例4: 证明幂函数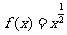 在
在 上是增函数.
上是增函数.
分析:直接根据函数单调性的定义来证明.
追踪训练二
1.下列函数中,在区间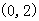 上是单调增函数的是
( )
上是单调增函数的是
( )
A.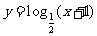 B.
B.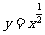
C.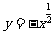 D.
D.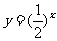
例3:已知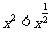 ,求
,求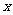 的取值范围.
的取值范围.
[解]在同一坐标系中作出幂函数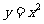 和
和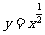 的图象,可得
的图象,可得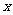 的取值范围为
的取值范围为 .
.
点评:数形结合的运用是解决问题的关键.
4、已知函数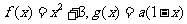 ,
,
当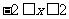 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
3、已知函数f(x)的定义域是(0,+∞),且对任意的x、y>0满足f(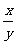 )=f(x)-f(y),当x>1时有f(x)<0,试判断f(x)的单调性并证明.
)=f(x)-f(y),当x>1时有f(x)<0,试判断f(x)的单调性并证明.
2、若函数f(x)满足f(x+y)+f(x-y)=f(x2-y2),则f(x)可以是( )
A.f(x)=2x B.f(x)=x2 C.f(x)=log2x D.f(x)=2x
例3: 已知: 在
在 上恒有
上恒有 ,求实数
,求实数 的取值范围。
的取值范围。
分析:去掉绝对值符号,转化为含对数式的不等式。
思维点拔:
本题的特点是给出了自变量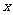 的取值范围,求字母
的取值范围,求字母 的取值范围,它与解不等式有
的取值范围,它与解不等式有
本质的区别,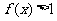 在
在 上恒成立,是指
上恒成立,是指 在
在
 上的所有值都大于1,这是一个不定问题,但转化为函数的最大(最小)值后,问题就简单了,这类问题的一般结论是:
上的所有值都大于1,这是一个不定问题,但转化为函数的最大(最小)值后,问题就简单了,这类问题的一般结论是:
(1)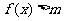 (
(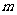 为常数,
为常数,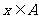 )恒成立,
)恒成立,


(2)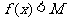 (
( 为常数,
为常数,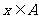 )恒成立,
)恒成立,


利用这两个结论,可以把“不定”问题转化为“定”的问题。
追踪训练
1、解不等式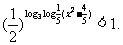
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com