
3、已知函数y=log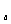 (3-ax)在[0,1]上是减函数,则a的取值范围是( )
(3-ax)在[0,1]上是减函数,则a的取值范围是( )
A.(0,1) B.(1,3) C.(0,3 ) D.[3,+∞)
2、函数y=2x与y=x2的图象的交点个数是( )
A.0个 B.1个 C.2个 D.3个
1、函数y=ax在[0,1]上的最大值与最小值的和为3,则a=( )
A.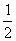 B.2 C.4 D.
B.2 C.4 D.
4、能解决一些函数的单调性、奇偶性等问题。
精典范例]
例1、已知f(x)=x3·(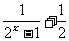 );
);
(1)判断函数的奇偶性;
(2)证明:f(x)>0.
例2、已知f(x)=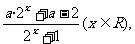 若f(x)满足f(-x)=-f(x).
若f(x)满足f(-x)=-f(x).
(1)求实数a的值;
(2)判断函数的单调性。
例3、已知f(x)=log (x+1),当点(x,y)在函数y=f(x)的图象上运动时,点(
(x+1),当点(x,y)在函数y=f(x)的图象上运动时,点(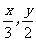 )在函数y=g(x)的图象上运动。
)在函数y=g(x)的图象上运动。
(1)写出y=g(x)的解析式;
(2)求出使g(x)>f(x)的x的取值范围;
(3)在(2)的范围内,求y=g(x) -f(x)的最大值。
例4、已知函数f(x)满足f(x2-3)=lg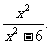
(1)求f(x)的表达式及其定义域;
(2)判断函数f(x)的奇偶性;
(3)当函数g(x)满足关系f[g(x)]=lg(x+1)时,求g(3)的值.
追踪训练
3、掌握图象的一些变换。
2、能运用指数函数,对数函数,幂函数的性质解决一些问题。
1、进一步巩固指数、函数,幂函数的基本概念。
3.求函数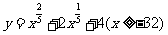 的值域.
的值域.
|
学生质疑 |
|
|
教师释疑 |
|

2.函数 在第二象限内单调递增,则
在第二象限内单调递增,则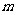 的最大负整数是
.
的最大负整数是
.
 例5:已知幂函数
例5:已知幂函数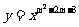 (
(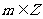 )的图象与
)的图象与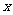 轴、
轴、 轴都无交点,且关于原点对称,求
轴都无交点,且关于原点对称,求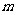 的值.
的值.
分析:幂函数图象与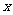 轴、
轴、 轴都无交点,则指数小于或等于零;图象关于原点对称,则函数为奇函数.结合
轴都无交点,则指数小于或等于零;图象关于原点对称,则函数为奇函数.结合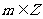 ,便可逐步确定
,便可逐步确定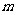 的值.
的值.
[
思维点拔:
(1)比较同指数幂的大小,利用幂函数的单调性;
(2)根据幂函数的图象,判断指数的大小,或根据幂函数的指数的大小,描述其图象的特征;
(3)判断幂函数的奇偶性,宜先将分数指数化为根式的形式.
追踪训练二
1.设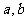 满足
满足 ,下列不等式中正确的是
( )
,下列不等式中正确的是
( )
A. B.
B. C.
C.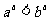 D.
D.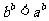
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com