例4: 利用指数的运算法则，解下列方程：

(1)4^3x+2=256×8^1－x

(2)2^x+2－6×2^x－1－8=0

解：(1)因为4^3x+2=256×8^1－x

所以2^6x+4=2⁸×2^3－3x

所以6x+4=11－3x

所以x=

(2)因为2^x+2－6×2^x－1－8=0

所以4×2^x－3×2^x－8=0

所以2^x=8

所以x=3

分析：利用分数指数幂的性质将方程两边转化为同底的指数幂.

[解](1)原方程可化为：，

，，∴

原方程的解为.

(2)原方程可化为：，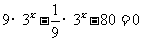

∴，，

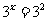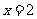
原方程的解为.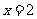

点评:将指数方程转化为一元一次或一元二次方程是解题的关键.

思维点拔：

(1)根式与分数指数幂运算要灵活地互化；(2)一般地在化简过程中，先将根式化为分数指数幂，然后利用同底运算性质进行运算.

追踪训练二

1．化简：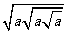

解：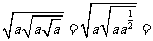

．

3．若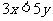，则

．

2．在①；②；③；④()各式中，有意义的是(　　)

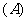①②　　①③　　①②③④　①③④

例4:解下列方程(1)；

(2)

分析：对原方程因式分解。

[解](1)原方程可化为，

∴，

原方程的根为。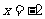

(2)原方程可化为，

∵，∴，

，，

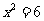原方程的根为。

点评:通过因式分解把原方程转化为二项方程，再利用根式意义求解。

思维点拔：

(1)求根式的值时要注意使根式有意义的被开方数的取值范围；(2)求形如的根式的值时要分清的奇偶性．

追踪训练二

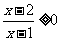
1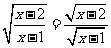．成立的条件是(　　)

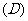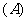
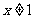
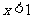
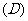
5、若f:y=3x+1是从集合A={1,2,3,k}到集合B={4,7,a⁴,a²+3a}的一个映射，该映射满足B中任何一个元素均有原象，求自然数a、k及集合A、B.

答案：a=2,　 k=5,　 A={1,2,3,5}　 B={4,7,10,16}

[师生互动]

4、已知映射f: A→B，其中集合A={－3，－2，－1，1，2，3，4}，集合B中元素都是A中的元素在映射f下的象，且对任意a∈A，在B中和它对应的元素是|a|，则集合B中的元素的个数是(　　 )

A.4　　　　　　　 B.5　　　　　　　　 C.6　　　　 D.7

答案：A

3、已知映射f: A→B,下面命题：

(1)A中的每一个元素在B中有且仅有一个象；

(2)A中不同的元素在B中的象必不相同；

(3)B中的元素在A中都有原象

(4)B中的元素在A中可以有两个以上的原象也可以没有原象。

假命题的个数是(　 )

A.1　　　　　　　 B.2　　　　　　　　 C.3　　　　　　　 D.4

答案：B

2、设f:A→B是集合A到B的映射，下列命题中是真命题的是(　　 )

A.A中不同元素必有不同的象

B.B中每一个元素在A中必有原象

C.A中每一个元素在B中必有象

D.B中每一个元素在A中的原象唯一

答案：C

例3、给出下列四个对应的关系

①A=N*,B=Z,f:x→y=2x－3；

②A={1，2，3，4，5，6}，B={y|y∈N*,y≤5}，f:x→y=|x－1|；

③A={x|x≥2}，B={y|y=x²－4x+3}，f:x→y=x－3；

④A=N,B={y∈N*|y=2x－1，x∈N*}，f:x→y=2x－1。

上述四个对应中是函数的有(　　 )

A.①　　　　　　　　　　 B.①③　　　　　　　　 C.②③　　　　　　　　 D.③④

思维分析：判断两个集合之间的对应是否构成函数，首先应判断能否构成映射，且构成映射的两个集合之间对应必须是非空数集之间的对应。

[解]：

①中，对x∈A，在f作用下，在B中都有唯一的象，因此能构成映射.由于A、B均为非空数集，因而能构成函数；②中，当x=1时,y=0B，即集合A中的元素1在集合B中无象，因而不能构成映射，从而也不能构成函数；④中，当x=0时，y=－1B，即0在B中无象，因而不能构成映射，也就不能构成函数；③中的两个对应符合映射的定义，且两个集合均为非空数集，因而能构成函数。

答案：B

[选修延伸]

求映射的个数问题

例4、已知A={a,b,c}，B={－1，0，1},映射f:A→B满足f(a)+f(b)=f(c)，求映射f: A→B的个数。

思维分析：可让A中元素在f下对应B中的一个、两个或三个元素，并且满足f(a)+f(b)=f(c)，需分类讨论。

[解]：(1)当A中三个元素都是对应0时，则f(a)+f(b)=0+0=0=f(c)有1个映射。

(2)当A中三个元素对应B中两个时，满足f(a)+f(b)=f(c)的映射有4个，分别为1+0=0，0+1=0，(－1)+0=－1,0+(－1)=－1.

(3)当A中的三个元素对应B中的三个元素时，有两个映射，分别为(－1)+1=0，1+(－1)=0.

因此满足题设条件的映射有7个。

追踪训练

1、下列对应是A到B上的映射的是(　 )

A.A=N*,B=N*,f:x→|x－3|

B.A=N*，B={－1,1, －2}，f:x→(－1)^x

C.A=Z,B=Q,f:x→

D.A=N*，B=R，f:x→x的平方根

答案：B

例2、已知集合A=R，B={(x,y)|x,y∈R}，f:A→B是从A到B的映射，f:x→(x+1,x²+1)，求A中的元素在B中的象和B中元素(,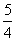)在A中的原象。

思维分析：将x=代入对应关系，可求出其在B中对应元素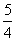，(,)在A中对应的元素可通过列方程组解出。

[解]：

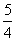将x=代入对应关系，可求出其在B中的对应元素(+1，3). 可通过列方程组也可求出(,)在A中对应的元素为