
3.求函数 的值域.
的值域.
答案:
|
学生质疑 |
|
|
教师释疑 |
|

2.函数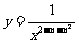 在第二象限内单调递增,则
在第二象限内单调递增,则 的最大负整数是
的最大负整数是 .
.
 例5:已知幂函数
例5:已知幂函数 (
( )的图象与
)的图象与 轴、
轴、 轴都无交点,且关于原点对称,求
轴都无交点,且关于原点对称,求 的值.
的值.
分析:幂函数图象与 轴、
轴、 轴都无交点,则指数小于或等于零;图象关于原点对称,则函数为奇函数.结合
轴都无交点,则指数小于或等于零;图象关于原点对称,则函数为奇函数.结合 ,便可逐步确定
,便可逐步确定 的值.
的值.
[解] ∵幂函数 (
( )的图象与
)的图象与 轴、
轴、 轴都无交点,
轴都无交点,
∴ ,∴
,∴ ;
;
∵ ,∴
,∴ ,又函数图象关于原点对称,
,又函数图象关于原点对称,
∴ 是奇数,∴
是奇数,∴ 或
或 .
.
点评: 掌握幂函数图象的特征,是顺利解题的关键.
思维点拔:
(1)比较同指数幂的大小,利用幂函数的单调性;
(2)根据幂函数的图象,判断指数的大小,或根据幂函数的指数的大小,描述其图象的特征;
(3)判断幂函数的奇偶性,宜先将分数指数化为根式的形式.
追踪训练二
1.设 满足
满足 ,下列不等式中正确的是
( C )
,下列不等式中正确的是
( C )
A. B.
B. C.
C.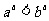 D.
D.
例4: 已知 ,求
,求 的取值范围.
的取值范围.
分析:数形给合思想的运用.由于不等式的左右两边的幂指数都是 ,因此可借助于幂函数
,因此可借助于幂函数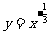 的图象性质来求解.
的图象性质来求解.
[解]因为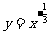 在
在 和
和 上为减函数,
上为减函数, 时,
时, ;
; 时,
时,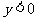 .原不等式可以化为
.原不等式可以化为
(1) (2)
(2)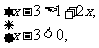
(3)
(1)无解;(2) ,(3)
,(3)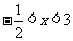
所以所求 的取值范围为
的取值范围为
{ }
}
点评:利用函数图象特征了解函数的性质,利用函数性质去解不等式.
4.证明:函数 在
在 上是减函数.
上是减函数.
证:略.
|
学生质疑 |
|
|
教师释疑 |
|
3.若 ,则
,则 的取值范围是 ( C )
的取值范围是 ( C )
A.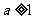 B.
B. C.
C. D.
D.
2.函数 的值域是 ( D )
的值域是 ( D )
A. B.
B. C.
C. D.
D.
例4: 证明幂函数 在
在 上是增函数.
上是增函数.
分析:直接根据函数单调性的定义来证明.
[解]证:设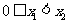 ,
,
则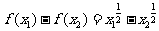


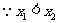


 即
即
 此函数在
此函数在 上是增函数
上是增函数
追踪训练二
1.下列函数中,在区间 上是单调增函数的是
( B )
上是单调增函数的是
( B )
A. B.
B.
C.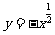 D.
D.
例3:已知 ,求
,求 的取值范围.
的取值范围.
[解]在同一坐标系中作出幂函数 和
和 的图象,可得
的图象,可得 的取值范围为
的取值范围为 .
.
点评:数形结合的运用是解决问题的关键.
4、已知函数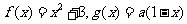 ,
,
当 时,
时, 恒成立,求实数
恒成立,求实数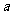 的取值范围。
的取值范围。
解:要使当 时,
时, 恒成立,即要:
恒成立,即要: 当
当 恒成立
恒成立
令


(1) 当 ,即
,即 时,
时, 得
得

(2) 当 ,即
,即 时,
时,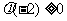 得
得
 (舍去)
(舍去)
(3) 当 ,即
,即 时,
时, 得
得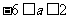
∴
由(1)(2)(3)可知,实数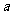 的取值范围为
的取值范围为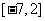 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com