
1.了解函数的零点与方程根的关系;
4.已知函数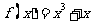
⑴试求函数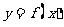 的零点;
的零点;
⑵是否存在自然数 ,使
,使 ?若存在,求出
?若存在,求出 ,若不存在,请说明理由.
,若不存在,请说明理由.
答案:(1)函数 的零点为
的零点为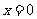 ;
;
(2)计算得 ,
, ,
,
由函数的单调性,可知不存在自然数 ,使
,使 成立.
成立.
|
学生质疑 |
|
|
教师释疑 |
|
3.已知函数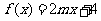 ,在
,在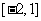 上存在
上存在 ,使
,使 ,则实数
,则实数 的取值范围是____
的取值范围是____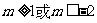 _____________.
_____________.
2.方程 的两个根分别在区间
的两个根分别在区间 和
和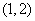 内,则
内,则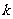 的取值范围是
的取值范围是 ;
;
例4:二次函数 中实数
中实数 、
、 、
、 满足
满足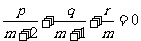 ,其中
,其中 ,求证:
,求证:
(1) );
);
(2)方程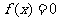 在
在 内恒有解.
内恒有解.
分析:本题的巧妙之处在于,第一小题提供了有益的依据: 是区间
是区间 内的数,且
内的数,且 ,这就启发我们把区间
,这就启发我们把区间 划分为(
划分为(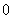 ,
, )和(
)和( ,
, )来处理.
)来处理.
[解](1)


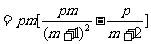
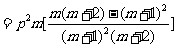
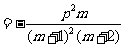 ,
,
由于 是二次函数,故
是二次函数,故 ,又
,又 ,所以,
,所以, .
.
⑵ 由题意,得 ,
, 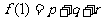 .
.
①当 时,由(1)知
时,由(1)知
 若
若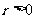 ,则
,则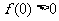 ,又
,又 ,所以
,所以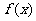 在(
在(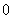 ,
, )内有解.
)内有解.
若 ,则
,则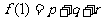
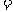


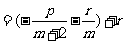
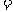
 ,又
,又 ,所以
,所以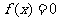 在(
在( ,
, )内有解.
)内有解.
②当 时同理可证.
时同理可证.
点评:(1)题目点明是“二次函数”,这就暗示着二次项系数 .若将题中的“二次”两个字去掉,所证结论相应更改.
.若将题中的“二次”两个字去掉,所证结论相应更改.
(2)对字母 、
、 分类时先对哪个分类是有一定讲究的,本题的证明中,先对
分类时先对哪个分类是有一定讲究的,本题的证明中,先对 分类,然后对
分类,然后对 分类显然是比较好.
分类显然是比较好.
追踪训练二
1.若方程 在
在 内恰有一则实数
内恰有一则实数 的取值范围是
(B )
的取值范围是
(B )
A. B.
B.
C. D.
D.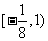
4. 已知二次函数 和一次函数
和一次函数 ,其中
,其中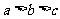 ,且
,且 ,
,
(1)求证:两函数 、
、 的图象交于不同两点
的图象交于不同两点 、
、 ;
;
(2)求线段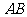 在
在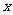 轴上投影
轴上投影 长度的取值范围.
长度的取值范围.
答案:(1)∵ ,
,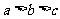 ,∴
,∴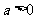 ,
, .由
.由 得
得 ,
,
因为 .
.
所以两函数 、
、 的图象必交于不同的两点;
的图象必交于不同的两点;
 (2)设
(2)设 ,
, ,则
,则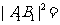
 .∵
.∵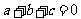 ,
,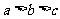 ,∴
,∴ .
.
∴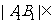 (
( ,
,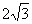 ).
).
|
学生质疑 |
|
|
教师释疑 |
|
3.不等式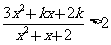 对一切实数
对一切实数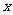 都立,则
都立,则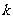 的取值范围是
的取值范围是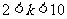 .
.
2.已知
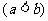 ,并且
,并且 、
、 是方程
是方程 的两个根
的两个根 ,则实数
,则实数 、
、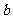 、
、 、
、 的大小关系可能是( A )
的大小关系可能是( A )
A. B.
B.
C. D.
D.
例4:已知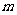 ,
, 是方程
是方程
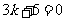 (
(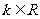 )的两个实根,求
)的两个实根,求 的最大值和最小值.
的最大值和最小值.
分析:一元二次方程与二次函数有很多内在联系.要求 的最值,首先要考虑根与系数的关系,并由此得到以
的最值,首先要考虑根与系数的关系,并由此得到以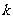 为自变量的
为自变量的 的函数解析式.
的函数解析式.
[解]因为方程 (
(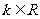 )有两个实根,所以
)有两个实根,所以
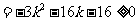 ,解得
,解得
又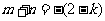 ,
,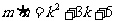 ,
,
所以

 .
.
 而
而 是减函数,因此当
是减函数,因此当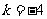 时,
时, 取最大值
取最大值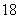 ,当
,当 时,
时, 取最小值
取最小值 .
.
点评:这是一个与一元二次方程根有关的问题,必须先确定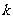 的取值范围,否则无法确定函数
的取值范围,否则无法确定函数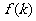 的单调性.
的单调性.
.
追踪训练二
1.
若方程 在
在 内恰有
内恰有
一解,则 的取值范围是( B )
的取值范围是( B )
A. B.
B.
C. D.
D.
例4: 已知函数 ,利用函数图象分别求它在下列区间上的值域:
,利用函数图象分别求它在下列区间上的值域:
(1) ; (2)
; (2)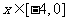 ; (3)
; (3)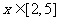 .
.
 [解]
[解]
(1) ;
;
(2) ;
;
(3) .
.
例5.集合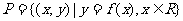 与集合
与集合 相同吗?请说明理由.
相同吗?请说明理由.
[解]不相等.集合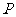 是坐标平面内的一个点集,表示函数
是坐标平面内的一个点集,表示函数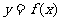 的图象;集合
的图象;集合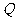 是一个数集,表示函数
是一个数集,表示函数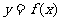 的值域.
的值域.
思维点拨
利用二次函数的图象求函数值域,作图时必须抓住以下关键点:抛物线的开口方向、对称轴、顶点以及区间的端点;解决集合问题,首先必须弄清集合中的元素是什么.
追踪训练二
1.已知函数f(x)=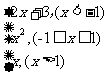
(1)画出函数图象;
(2)求f{f[f(-2)]}
(3)求当f(x)= -7时,x的值;
解:(1)图象略
(2)f(-2)=2x(-2)+3=-1
f(-1)=( -1)2=1
f(1)=1
所以f{f[f(-2)]}=1
(3)因为f(x)= -7
所以2x+3=-7
所以x=-5
|
学生质疑 |
|
|
教师释疑 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com