
5.已知方程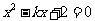 在区间
在区间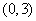 中有且只有一解,则实数
中有且只有一解,则实数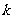 的取值范围为
的取值范围为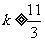 .
.
|
学生质疑 |
|
|
教师释疑 |
|
4.函数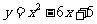 与
与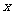 轴交点坐标是
轴交点坐标是 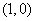 、
、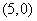 ,方程
,方程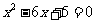 的根为
的根为 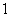 或
或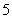 .
.
3. 直线
直线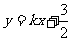 与曲线
与曲线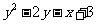
 只有一个公共点,则k的值为( A )
只有一个公共点,则k的值为( A )
A. 0,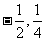 B. 0,
B. 0,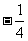
C. 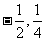 D. 0,
D. 0,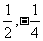
2.已知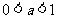 则方程
则方程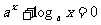 的解的个数是(
A )
的解的个数是(
A )
A.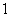 B.
B. 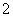 C.
C.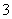 D. 不确定
D. 不确定
1.函数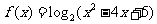 的图象与
的图象与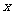 轴交点横坐标为 ( D )
轴交点横坐标为 ( D )
)
A.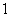 B.
B. C.
C.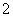 或
或 D.
D. 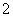
3.二分法求方程的近似解
 二分法求方程的近似解,首先要找到方程的根所在的区间
二分法求方程的近似解,首先要找到方程的根所在的区间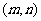 ,则必有
,则必有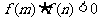 ,再取区间的中点
,再取区间的中点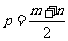 ,再判断
,再判断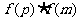 的正负号,若
的正负号,若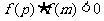 ,则根在区间
,则根在区间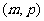 中;若
中;若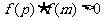 ,则根在
,则根在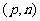 中;若
中;若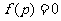 ,则
,则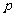 即为方程的根.按照以上方法重复进行下去,直到区间的两个端点的近似值相同(且都符合精确度要求),即可得一个近似值.
即为方程的根.按照以上方法重复进行下去,直到区间的两个端点的近似值相同(且都符合精确度要求),即可得一个近似值.
[精典范例]
例1:已知二次函数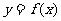 的图象经过点
的图象经过点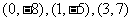 三点,
三点,
(1)求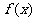 的解析式;
的解析式;
(2)求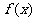 的零点;
的零点;
(3)比较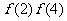 ,
, ,
,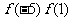 ,
,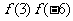 与
与 的大小关系.
的大小关系.
分析:可设函数解析式为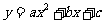 ,将已知点的坐标代入方程解方程组求
,将已知点的坐标代入方程解方程组求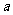 、
、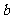 、
、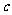 .
.
[解](1)设函数解析式为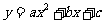 ,
,
由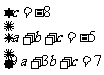 解得
解得 ,
,
∴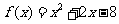 .
.
(2)令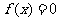 得
得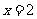 或
或 ,
,
∴零点是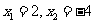 .
.
(3)
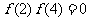 ,
,
 ,
,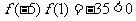 ,
,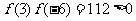 .
.
点评:当二次函数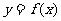 的两个零点
的两个零点
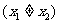 都在(或都不在)区间
都在(或都不在)区间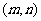 中时,
中时,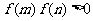 ;有且只有一个零点在区间
;有且只有一个零点在区间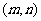 中时,
中时,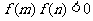 .
.
例2:利用计算器,求方程 的近似解(精确到
的近似解(精确到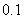 ).
).
分析一:可先找出方程的根所在的一个区间,再用二分法求解.
解法一:设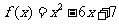 ,通过观察函数的草图得:
,通过观察函数的草图得:
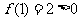 ,
,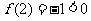 ,
,
∴方程 有一根在
有一根在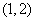 内,设为
内,设为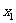 ,
,
∵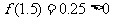 ,∴
,∴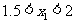 ,
,
又∵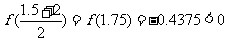 ,∴
,∴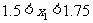 ,如此继续下去,得
,如此继续下去,得
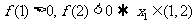 ,
,
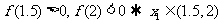 ,
,
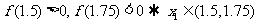
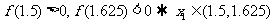
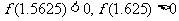
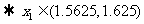
∵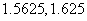 精确到
精确到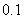 的近似值都为
的近似值都为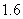 ,所以方程
,所以方程 的一个近似值都为
的一个近似值都为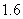 ,用同样的方法,可求得方程的另一个近似值为
,用同样的方法,可求得方程的另一个近似值为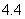 .
.
点评:解题过程中要始终抓住重点:区间两端点的函数值必须异号.
分析二:还可以用方程近似解的另一种方法--“迭代法”来求解.
 解法二:将原方程写成
解法二:将原方程写成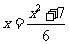 ①
①
取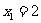 代入等式右边得
代入等式右边得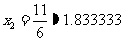 ,再将
,再将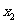 代入方程①右边,得
代入方程①右边,得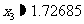 ,……
,……
如此循环计算数十次后,可得计算结果稳定在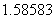 ,∴该方程的近似解为
,∴该方程的近似解为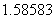 ,精确到
,精确到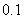 后为
后为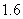 .用同样的方法可以求出方程的另一个近似解为
.用同样的方法可以求出方程的另一个近似解为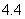 .
.
点评:“迭代法”也是一种常用的求近似解的方法.
例3:已知函数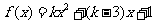 的图象与
的图象与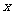 轴在原点的右侧有交点,试确定实数
轴在原点的右侧有交点,试确定实数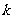 的取值范围.
的取值范围.
分析:
[解](1)当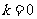 时,
时, 与
与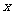 轴的交点为
轴的交点为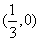 ,符合题意;
,符合题意;
(2)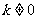 时,
时,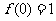 ,
,
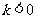 时,
时,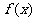 的图象是开口向下的抛物线,它与
的图象是开口向下的抛物线,它与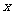 轴的两交点分别在原点的两侧;
轴的两交点分别在原点的两侧;
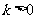 时,
时,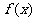 的图象是开口向上的抛物线,必须
的图象是开口向上的抛物线,必须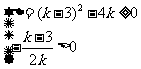 ,解得
,解得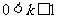
综上可得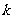 的取值范围为
的取值范围为 .
.
追踪训练一
2.函数与方程
两个函数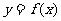 与
与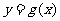 图象交点的横坐标就是方程
图象交点的横坐标就是方程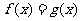 的解;反之,要求方程
的解;反之,要求方程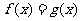 的解,也只要求函数
的解,也只要求函数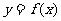 与
与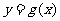 图象交点的横坐标.
图象交点的横坐标.
1.一元二次函数与一元二次方程
一元二次函数与一元二次方程(以后还将学习一元二次不等式)的关系一直是高中数学函数这部分内容中的重点,也是高考必考的知识点.我们要弄清楚它们之间的对应关系:一元二次函数的图象与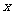 轴的交点的横坐标是对应一元二次方程的解;反之,一元二次方程的解也是对应的一元二次函数的图象与
轴的交点的横坐标是对应一元二次方程的解;反之,一元二次方程的解也是对应的一元二次函数的图象与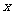 轴的交点的横坐标.
轴的交点的横坐标.
3.体会函数与方程的内在联系,初步建立用函数方程思想解决问题的思维方式.
自学评价
2.根据具体的函数图象,能够用二分法求相应方程的近似解;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com