
10.解:(1)定义域: 得:
得:
(2)∵
∴当 ,
, ,函数的值域为
,函数的值域为 .
.
当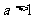 时,
时,  ,函数的值域为
,函数的值域为 .
.
(3)∵ 在区间内
在区间内 在
在 上递增,在
上递增,在 上递减.
上递减.
当 时,函数在
时,函数在 上是减函数,在
上是减函数,在 是增函数.
是增函数.
当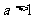 时,函数在
时,函数在 上是增函数,在
上是增函数,在 是减函数.
是减函数.
9.(1)令 ,得
,得 ;
;
(2) ,
,
∴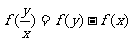 ;
;
(3)设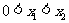 ,则
,则 ,
,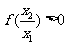 ,
,
又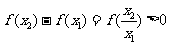 ,
,
∴ ;
;
函数 在定义域
在定义域 上是增函数.
上是增函数.
6. 7.(1)
7.(1)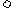 (2)
(2)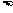 (3)
(3) (4)
(4) 8.
8.
1. 2.
2. 3.
3. 4.
4. 5.
5.
11.分析:第2小题 的取值必须使得定义域是二次函数单调增区间的子区间,因此,第1小题求函数定义域的环节至关重要,不求定义域或定义域求错都将导致第2小题的错误.
的取值必须使得定义域是二次函数单调增区间的子区间,因此,第1小题求函数定义域的环节至关重要,不求定义域或定义域求错都将导致第2小题的错误.
解答:(1)设商品现在定价 元,卖出的数量为
元,卖出的数量为 个.
个.
由题设:当价格上涨x%时,销售总额 ,
,
即 (
(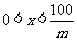 ),
),
取 得:
得: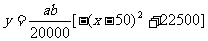 ,
,
当 时,
时, ,
,
即该商品的价格上涨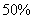 时,销售总金额最大.
时,销售总金额最大.
(2)二次函数 在
在  上递增,
上递增,
在 上递减,
上递减,
适当地涨价能使销售总金额增加,即在 内存在一个区间,使函数
内存在一个区间,使函数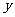 在此区
在此区
间上是增函数,所以  ,
,
解得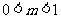 ,
,
即所求 的取值范围是
的取值范围是 .
.
点评: 求定义域时考虑到销售量必须大于 的事实,得出了最确切的定义域,为后面继续解题打下基础.
的事实,得出了最确切的定义域,为后面继续解题打下基础.
10.这种商品的日销售额的最大值为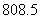 . 分情况讨论.
. 分情况讨论.
7. 8.
8. 9.
9.
6.(1) 小时,
小时,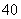 吨; (2)
吨; (2) 小时.
小时.
3.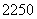 4.
4. 5.
5.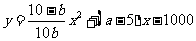
13.作出函数 ,
, 的图象,观察图象发现,在区间
的图象,观察图象发现,在区间 上,模型
上,模型 的图象都有一部分在直线
的图象都有一部分在直线 的上方,只有模型
的上方,只有模型 的图象始终在直线
的图象始终在直线 的下方,这说明只有按照模型
的下方,这说明只有按照模型 进行奖励才符合公司的要求.下面通过计算确认:
进行奖励才符合公司的要求.下面通过计算确认:
对于模型 ,在区间
,在区间 上递增,当
上递增,当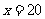 时,
时, ,当
,当 时,
时, ,所以该模型不符合要求.
,所以该模型不符合要求.
对于模型 ,在区间
,在区间 上递增,由图象和计算可知,在区间
上递增,由图象和计算可知,在区间 内有一个点
内有一个点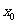 满足
满足 ,∴当
,∴当 时,
时, ,所以该模型也不符合要求.
,所以该模型也不符合要求.
对于模型 ,它在区间
,它在区间 上递增,且当
上递增,且当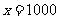 时,
时,
 ,∴它符合奖金总数不超过
,∴它符合奖金总数不超过 万元的要求.又当
万元的要求.又当 时,令
时,令 ,它在区间
,它在区间 上递减,
上递减,
∴ ,即
,即 ,
,
所以按模型 奖励,奖金不超过利润的
奖励,奖金不超过利润的 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com