
6.下列函数中,有反函数的是( )
A.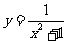 B.
B. C.
C. D.
D.





5.已知函数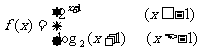 ,若
,若 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.

4.要得到函数 的图象,只需要把函数
的图象,只需要把函数 的图象
( )
的图象
( )
A.向左平移 个单位
B.向右平移
个单位
B.向右平移 个单位
个单位
C.向左平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
3.已知 ,则“
,则“ ”是“
”是“ ”的
(
)
”的
(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知等差数列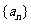 的前
的前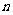 项和为
项和为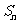 ,且
,且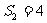 ,
, ,则
,则 ( )
( )
A. B.
B.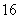 C.
C. D.
D.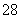

1.已知全集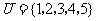 ,集合
,集合 ,
, ,则集合
,则集合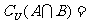 ( )
( )
A.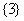 B.
B. C.
C. D.
D.

1、 书本 P 93 随堂练习 1、2 《练习册》 P 45
四、 小结
垂径定理及其逆定理。
五、 作业
书本 P 94 习题3.2 1
六、 教学后记
3、 进一步体会和理解研究几何图形的各种方法
教学重点和难点
重点:垂径定理及其逆定理 难点:垂径定理及其逆定理
教学过程设计
一、 从学生原有的认知结构提出问题
圆是我们比较熟悉的图形。它是漂亮的图形,这节课,我们研究一下它的性质。
二、
 师生共同研究形成概念
师生共同研究形成概念
1、 圆的轴对称性
☆ 议一议 书本P 89
在探索圆是轴对称图形时,大多数学生可能会采用折叠的方法,有的学生也可能用其他方法,只要合理,都应该鼓励
圆是轴对称图形,其对称轴是任意一条过圆心的直线
2、 圆的几个概念
|
|
|
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧 优弧DCA 劣弧AB
连接圆上任意两点的线段叫做弦
经过圆心的弦叫做直径
² 注意
 直径是弦,但弦不一定是直径;半圆是弧,但弧不一定是半圆;半圆既不是劣弧,也不是优弧
直径是弦,但弦不一定是直径;半圆是弧,但弧不一定是半圆;半圆既不是劣弧,也不是优弧
3、 垂径定理
☆ 做一做 书本P 90 做一做
从此例子得出垂径定理。
垂直于弦的直径平分这条弦,并且平分弦所对的弧
如图,在⊙O中,直径CD⊥弦AB,垂足为M,
(1)
|
|
(2) 若AB = 10,则AM = ,BC = 5,则AC = 。
4、 讲解例题
例1  如图,AB是⊙O的一条弦,OC⊥AB于点C,OA = 5,AB = 8,求OC的长。
如图,AB是⊙O的一条弦,OC⊥AB于点C,OA = 5,AB = 8,求OC的长。
5、 垂径定理的逆定理
☆ 想一想 书本P 91 想一想
 鼓励学生独立探索,然后通过同学间的交流,得出结论。
鼓励学生独立探索,然后通过同学间的交流,得出结论。
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
如图,在⊙O中,直径CD平分弦AB,交AB于点M,
(1)
|
|
(2) 若BC = 5,则AC = 。
6、 讲解例题
例2 如图,AB是⊙O的一条弦,点C为弦AB的中点,OC = 3,AB = 8,求OA的长。
例3  如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系?为什么?
如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系?为什么?
 |
|||||
|
|||||
|
|||||
例4 
|
三、 随堂练习
2、 理解圆的对称性及相关性质
1、 经历探索圆的对称性及相关性质,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com