
1、曲线 关于直线
关于直线 对称的直线方程为
( )
对称的直线方程为
( )
A、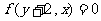 B、
B、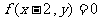 C、
C、 D、
D、
1、如果实数 满足等式
满足等式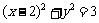 ,那么
,那么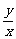 的最大值是
( )
的最大值是
( )
A、 B、
B、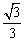 C、
C、 D、
D、
1.使圆x2+y2=r2与x2+y2+2x-4y+4=0有公共点则( )
A.r< +1 B.r>
+1 B.r> +1 C.|r-
+1 C.|r- |<1 D.|r-
|<1 D.|r- |≤1
|≤1
2x2+y2-2x+4y-20=0截直线5x-12y+c=0所得的弦长为8,则c的值是
[精典范例]
例题1.过点(2,1)并与两坐标轴都相切的圆的方程是
例2:..若动圆C与圆(x-2)2+y2=1外切,且和直线x+1=0相切.求动圆圆心C的轨迹E的方程
[解]
 例3:已知圆C:x2+y2-2x+4y-4=0,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点.若存在,求出直线l的方程;若不存在,说明理由
例3:已知圆C:x2+y2-2x+4y-4=0,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点.若存在,求出直线l的方程;若不存在,说明理由
[解]
[选修延伸]
例4:设圆满足(1)y轴截圆所得弦长为2.(2)被x轴分成两段弧,其弧长之比为3∶1,在满足(1)、(2)的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
[解]

思维点拔:在解决直线与圆的位置关系的问题时,我们通常采用“几何法”.例如,求与圆相切的直线方程时,先用待定系数法设出直线方程,然后根据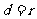 即可求得.这种数形结合的思想贯穿了整个章节.
即可求得.这种数形结合的思想贯穿了整个章节.
追踪训练
2.掌握圆以及直线与圆的位置关系.
自学评价

学习要求
1.掌握直线的几种形式与应用;
2.已知三角形ABC的三个顶点A(2,-1,4),B(3,2,-6),C(-5,0,2),求:
(1)BC的中点M的坐标;(2)三角形ABC的中线的长度.
|
学生质疑 |
|
|
教师释疑 |
|
例4: 讨论方程
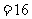 的几何意义.
的几何意义.
[解]
思维点拔:
注意类比在解决一些空间问题中的应用.
追踪训练二
1. 试解释方程
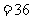 的几何意义.
的几何意义.
例4: 求点 关于
关于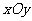 平面,
平面, 平面及原点的对称点.
平面及原点的对称点.
[解]
追踪训练二
1. 写出分别在坐标轴、坐标平面上的点 的坐标所满足的条件.
的坐标所满足的条件.
|
学生质疑 |
|
|
教师释疑 |
|
2.已知一个圆经过直线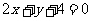 与圆
与圆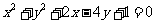 的两个交点,并且有最小面积,求此圆的方程.
的两个交点,并且有最小面积,求此圆的方程.
|
学生质疑 |
|
|
教师释疑 |
|
1.一个圆经过圆 和圆
和圆 的两个交点,且圆心在直线
的两个交点,且圆心在直线 上,求该圆的方程.
上,求该圆的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com