3. 三条直线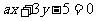，，有且只有两个交点，则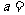

______________．

[选修延伸]

例4: 已知三条直线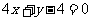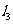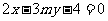：，：，：，求分别满足下列条件的的值：

(1)使这三条直线交于同一点；

(2)使这三条直线不能构成三角形．

例5：求证：不论为何实数，直线：恒过一定点，并求出此定点的坐标．

思维点拔：

因为直线上点的坐标就是对应方程的解,所以两直线是否有交点,取决于它们对应方程组成的方程组是否有唯一解.体验“形”的问题怎样通过“数”的运算来解决,从而感悟到解析几何的本质(即用代数的方法来研究或解决几何问题).

追踪训练二

2. 若三条直线 相交于一点，则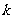的值等于　　　　　　　　　　 (　 　　)

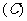
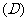
1. 若一条直线过点(2,1)，且与另一条直线相交于点(1,2),则该直线的方程为______________________．

3．学生通过一般形式的直线方程解的讨论，加深对解析法的理解，培养转化能力

自学评价

(1)求两直线的交点坐标只需将这两条直线的方程联立成方程组，_______________即为交点坐标.

(2)在解由两直线的方程组成的方程组的时候可能出现的三种结果是：

①方程组有一组解，该解为_____________；

②方程组有无数组解，此时两直线的位置关系为________，交点个数为_____________；

③方程组无解，此时两直线的位置关系是 _________，交点个数为___________．

[精典范例]

例1：分别判断下列直线是否相交，若相交，求出它们的交点：

(1):，:；

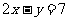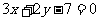(2):，

:；

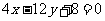(3):，:．

例2：直线经过原点，且经过另外两条直线，的交点，求直线的方程．

例3：某商品的市场需求(万件)、市场供求量(万件)、市场价格(元/件)分别近似地满足下列关系：．当时的市场价格称为市场平衡价格，此时的需求量称为平衡需求量．

(1)求市场平衡价格和平衡需求量；

(2)若要使平衡需求量增加4万件，政府对每件商品应给予多少元补贴？

追踪训练一

2．当两条直线相交时，会求交点坐标；

1．知道两条直线的相交、平行和重合三种位置关系，对应于相应的二元一次方程组有唯一解、无解和无穷多组解；

4．分别经过点A(1,2)、B(2,4)的两条直线互相平行，当它们之间的距离达到最大时，求这两条直线的方程．

[师生互动]

3．过点的所有直线中，距离原点最远的直线方程是_______________________．

2．由四条直线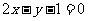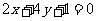：，，，围成的四边形是　　　　　　　　　　　　　　　　 (　　 )

等腰梯形梯形 长方形正方形

1．若直线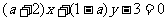与互相垂直，则实数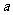的值为___________________．