
1. 以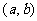 为圆心,
为圆心,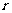 为半径的圆的标准方程:
为半径的圆的标准方程: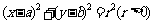 .
.
3.能根据所给条件,通过求半径和圆心的方法求圆的标准方程.
[课堂互动]
自学评价
2.掌握圆的标准方程,并能根据方程写出圆心的坐标和圆的半径;
1.认识圆的标准方程并掌握推导圆的方程的思想方法;
例5:分别过 两点作两条平行线,求满足下列条件的两条直线方程:
两点作两条平行线,求满足下列条件的两条直线方程:
(1)两平行线间的距离为 ;(2)这两条直线各自绕
;(2)这两条直线各自绕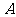 、
、 旋转,使它们之间的距离取最大值.
旋转,使它们之间的距离取最大值.
 分析:(1)两条平行直线分别过
分析:(1)两条平行直线分别过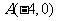 ,
,
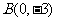 两点,因此可以设出这两条直线的方程之间(注意斜率是否存在),再利用两条平行直线之间的距离公式,列出方程,解出所要求的直线的斜率;(2)这两条平行直线与
两点,因此可以设出这两条直线的方程之间(注意斜率是否存在),再利用两条平行直线之间的距离公式,列出方程,解出所要求的直线的斜率;(2)这两条平行直线与 垂直时,两直线之间距离最大.
垂直时,两直线之间距离最大.
[解](1)当两直线的斜率不存在时,方程分别为 ,满足题意.
,满足题意.
当两直线的斜率存在时,设方程分别为
 与
与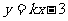 ,
,
即: 与
与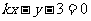 ,由题意:
,由题意: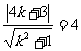 ,解得
,解得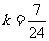 ,
,
所以,所求的直线方程分别为:
 ,
,  .
.
综上:所求的直线方程分别为:
 ,
,
或 .
.
(2)结合图形,当两直线与 垂直时,两直线之间距离最大,最大值为
垂直时,两直线之间距离最大,最大值为 ,同上可求得两直线的方程.此时两直线的方程分别为
,同上可求得两直线的方程.此时两直线的方程分别为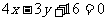 ,
, .
.
点评:(1)设直线方程时一定要先考虑直线的斜率是否存在,利用平行直线之间的距离公式列出相应的方程,解出相应的未知数;(2)体现了数形结合的思想,通过图形,发现问题的本质.
思维点拔:对称问题
在遇到对称问题时关键是分析出是属于什么对称情况,这里大致可以分为:点关与点对称,点关于直线对称,直线关于点对称,直线关于直线对称这四种情况,一旦确定为哪种情况后对应本节课的四种基本方法进行求解.
追踪训练二
1.两平行直线 ,
, 分别过
分别过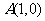 ,
,
(1) ,
, 之间的距离为5,求两直线方
之间的距离为5,求两直线方
程;
(2)若 ,
, 之间的距离为
之间的距离为 ,求
,求 的取值范围.
的取值范围.
[解](1)当两直线的斜率不存在时,方程分别为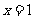 ,
, ,不满足题意.
,不满足题意.
当两直线的斜率存在时,设方程分别为
 与
与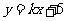 ,
,
即: 与
与 ,
,
由题意: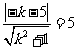 ,解得
,解得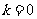 或
或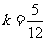 ,
,
所以,所求的直线方程分别为:
 :
: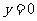 ,
, :
: 或
或
 :
: ,
,
 :
: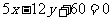 .
.
(2) .
.
|
学生质疑 |
|
|
教师释疑 |
|

2. 两条平行直线
两条平行直线 :
: ,
, :
: (
( )之间的距离:
)之间的距离: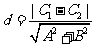 使用该公式时应该注意:
使用该公式时应该注意:
两条平行直线 与
与 的形式必须是一般式,同时
的形式必须是一般式,同时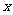 和
和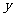 前面的系数必须化为一致.
前面的系数必须化为一致.
|
学生质疑 |
|
|
教师释疑 |
|

1.点 到直线
到直线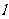 :
: (
( ,
, 不同时为
不同时为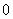 )
)
的距离: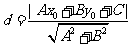 .使用该公式时应该注意:
.使用该公式时应该注意:
(1)公式中的直线方程必须化为一般式;(2)若点 在直线
在直线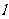 上,则
上,则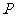 到直线
到直线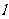 的距离为
的距离为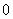 ,此时公式仍适用;
,此时公式仍适用;
(3)特别地,点 到
到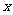 轴的距离为
轴的距离为 ,到
,到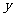 轴的距离为
轴的距离为 .
.
4.已知平行线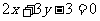 与
与
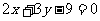 ,求与它们等距离的平行线的方程.
,求与它们等距离的平行线的方程.
[解]设所求直线方程为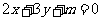 ,
,
由题意可得,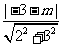
 ,解得
,解得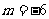 .
.
所以,所求的直线方程为: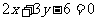
思维点拔:
3.  :
: ,
,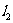 :
:
之间的距离为 .
.
2. 直线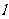 过点
过点 ,且与原点的距离等于
,且与原点的距离等于 ,则直线
,则直线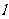 的方程为:
的方程为: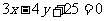 或
或 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com