
例3: 已知圆 ,圆
,圆 ,求两圆的公共弦所在的直线方程及公共弦长.
,求两圆的公共弦所在的直线方程及公共弦长.
分析:因两圆的交点坐标同时满足两个圆方程,联立方程组,消去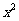 项、
项、 项,即得两圆的两个交点所在的直线方程,利用勾股定理可求出两圆公共弦长.
项,即得两圆的两个交点所在的直线方程,利用勾股定理可求出两圆公共弦长.
[解]设两圆交点为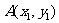 、
、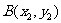 ,则
,则 两点坐标满足方程组
两点坐标满足方程组
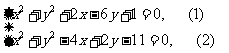 ,
,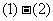 得
得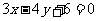 .
.
因为, 两点坐标都满足此方程,
两点坐标都满足此方程,
所以,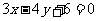 即为两圆公共弦所在的直线方程.
即为两圆公共弦所在的直线方程.
易知圆 的圆心
的圆心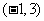 ,半径
,半径 .
.
又 到直线的距离为
到直线的距离为
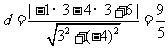 .所以,
.所以,
 .即两圆的公共弦长为
.即两圆的公共弦长为 .
.
点评:本题较为复杂,要讨论的情况比较多,解题过程中要 注重分析.
例5:求过两圆
 的交点,且圆心在直线
的交点,且圆心在直线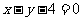 上的圆的方程.
上的圆的方程.
分析:所求圆圆心是两已知圆连心线和已知直线的交点,再利用弦心距、弦长、半径之间的关系求圆半径
[解](法一)可求得两圆连心线所在直线的方程为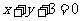 .
.
由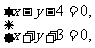 得圆心
得圆心 .
.
利用弦心距、弦长、半径之间的关系可求得公共弦长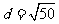 , 所以,圆半径
, 所以,圆半径
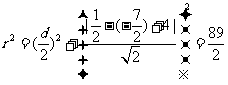 .
.
 所以,所求圆方程为
所以,所求圆方程为 ,
,
即
(法二)设所求圆的方程为 即
即 .
.
故此圆的圆心为 ,它在直线
,它在直线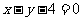 上, 所以
上, 所以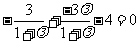 ,所以
,所以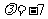 .
.
所以所求圆方程为
点评:“解法二”中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程.
思维点拔:
解题时要充分利用两圆位置关系的几何性质.
追踪训练二
1.一个圆经过圆 和圆
和圆 的两个交点,且圆心在直线
的两个交点,且圆心在直线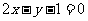 上,求该圆的方程.
上,求该圆的方程.
答案: .
.
2.若直线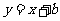 与
与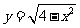 有两个不同的交点,求实数
有两个不同的交点,求实数 的取值范围.
的取值范围.
答案: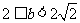 .
.
例4: 已知圆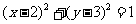 ,求该圆与
,求该圆与 轴和
轴和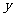 轴的截距相等的切线
轴的截距相等的切线 的方程.
的方程.
分析:用待定系数法求解.
[解]由题意设切线 与
与 轴和
轴和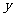 轴的截距为
轴的截距为 ,
, ,则
,则
① 时,设
时,设 的方程为
的方程为 ,即
,即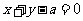 ,
,
因为直线和圆相切,所以圆心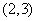 到直线
到直线 的距离等于圆的半径,故
的距离等于圆的半径,故
 解得
解得 或
或
所以 的方程为
的方程为 或
或
② 时,设
时,设 的方程为
的方程为 ,即
,即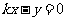
所以 ,解得
,解得 或
或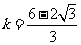
所以 的方程为
的方程为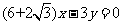 或
或
综上所述: 的方程为
的方程为 或
或 或
或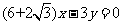 或
或
 .
.
点评:本题较为复杂,要讨论的情况比较多,解题过程中要注重分析.
 例5:若直线
例5:若直线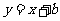 与
与 恰有一个公共点,求实数
恰有一个公共点,求实数 的取值范围.
的取值范围.
分析:由题意 可化为
可化为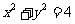
 表示一个右半圆,如图所示,对于
表示一个右半圆,如图所示,对于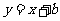 当
当 变化时所得的直线是互相平行的,由图可知
变化时所得的直线是互相平行的,由图可知 与半圆有一个交点
与半圆有一个交点
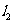 与半圆正好有两个交点,所以位于
与半圆正好有两个交点,所以位于 和
和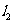 之间的直线都与半圆只有一个交点,另外
之间的直线都与半圆只有一个交点,另外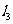 与半圆相切也符合题意
与半圆相切也符合题意
 [解]由题意
[解]由题意 可化为
可化为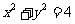

表示一个右半圆,如图所示
直线 的方程为:
的方程为: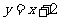 ,
,
直线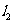 的方程为:
的方程为: ,
,
|
学生质疑 |
|
|
教师释疑 |
|
因为直线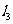 与半圆相切,
与半圆相切,
所以 ,解得
,解得
所以直线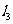 的方程为:
的方程为: ,
,
由图可知位于 和
和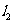 之间的直线都与半圆只有一个交点,且
之间的直线都与半圆只有一个交点,且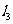 与半圆相切,
与半圆相切,
所以实数 的取值范围为:
的取值范围为:
 或
或
点评:本题应用数形结合的方法去解题.
思维点拔:
在解决直线与圆的位置关系的问题时,我们通常采用“几何法”.例如,求与圆相切的直线方程时,先用待定系数法设出直线方程,然后根据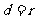 即可求得.这种数形结合的思想贯穿了整个章节.
即可求得.这种数形结合的思想贯穿了整个章节.
追踪训练二
1.已知圆 ,求该圆与
,求该圆与 轴和
轴和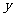 轴的截距的绝对值相等的切线
轴的截距的绝对值相等的切线 的方程.
的方程.
答案: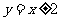 或
或 .
.
4.求圆 关于直线
关于直线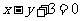 对称的图形的方程.
对称的图形的方程.
[解] 可化为
可化为
 ,圆心
,圆心 关于直线
关于直线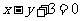 的对称点为
的对称点为 ,所以对称的图形的方程为:
,所以对称的图形的方程为: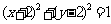 .
.
思维点拔:
在确定圆的方程时,应根据已知条件与圆的标准方程和圆的一般方程的各自特点,灵活选用圆方程的形式.在解题时注意运用平面几何知识及数形结合的思想.
|
学生质疑 |
|
|
教师释疑 |
|

3. 求过三点 的圆的方程.
的圆的方程.
[解]设圆的方程为
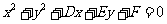 ,
,
∵ ,
,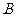 ,
, 三点都在圆上,
三点都在圆上,
∴ ,
,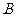 ,
, 三点坐标都满足所设方程,把
三点坐标都满足所设方程,把 代入所设方程,
代入所设方程,
得: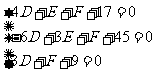 ,
,
解得: ,所以,所求圆的方程为:
,所以,所求圆的方程为: .
.
2.圆 的圆心为:
的圆心为: ,半径为
,半径为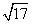 .
.
1.下列方程各表示什么图形?
(1)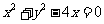 ;
;
(2) ;
;
(3) .
.
[解](1)圆心为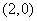 ,半径为2的圆;
,半径为2的圆;
(2)一个点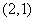 ;
;
(3)一个圆心为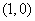 ,半径为
,半径为 的一个半圆(
的一个半圆(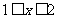 )(图略).
)(图略).
4.圆的一般方程:
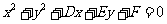
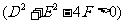 .
.
注意:对于圆的一般方程
(1) 和
和 的系数相等,且都不为
的系数相等,且都不为 (通常都化为
(通常都化为 );
);
(2)没有 这样的二次项;
这样的二次项;
 (3)表示圆的前提条件:
(3)表示圆的前提条件:
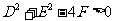 ,通常情况下先配方配成
,通常情况下先配方配成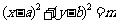 ,通过观察
,通过观察 与
与 的关系,观察方程是否为圆的标准方程,而不要死记条件
的关系,观察方程是否为圆的标准方程,而不要死记条件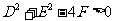 .
.
[精典范例]
例1:求过三点 的圆的方程.
的圆的方程.
分析:由于 不在同一条直线上,因此经过
不在同一条直线上,因此经过 三点有唯一的圆.
三点有唯一的圆.
[解]:法一:设圆的方程为
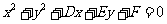 ,
,
∵ 三点都在圆上,
三点都在圆上,
∴ 三点坐标都满足所设方程,把
三点坐标都满足所设方程,把 代入所设方程,
代入所设方程,
得: ,
,
解得: ,
,
所以,所求圆的方程为:
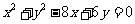 .
.
法二:也可以求 和
和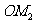 中垂线的交点即为圆心,圆心到
中垂线的交点即为圆心,圆心到 的距离就是半径也可以求的圆的方程:
的距离就是半径也可以求的圆的方程: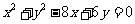 .
.
点评:通常在求圆心与半径方便时用标准方程,在已知圆三个点时通常用一般方程求解.
例2:已知线段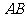 的端点
的端点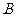 的坐标是
的坐标是
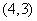 ,端点
,端点 在圆
在圆 上运动,求线段
上运动,求线段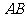 中点
中点 的坐标
的坐标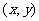 中
中 满足的关系?并说明该关系表示什么曲线?
满足的关系?并说明该关系表示什么曲线?
分析:线段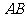 的端点
的端点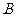 静止,
静止, 在圆
在圆
 上运动,因此我们可以设出
上运动,因此我们可以设出 的坐标,从而得到中点
的坐标,从而得到中点 的坐标.
的坐标.
[解]设点 的坐标是
的坐标是 ,由于点
,由于点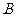 的坐标是
的坐标是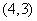 ,且
,且 是
是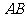 的中点,所以
的中点,所以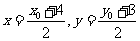 (*)
(*)
于是,有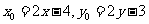
因为点 在圆
在圆 上运动,所以点
上运动,所以点 的坐标满足方程
的坐标满足方程 ,
,
即: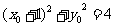 (**),
(**),
将(*)式代入(**),得:
 ,
,
整理得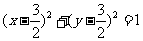
所以 满足的关系为:
满足的关系为: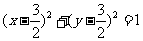 ,
,
其表示的曲线是以 为圆心,1为半径的圆.
为圆心,1为半径的圆.
点评: 该圆就是 点的运动的轨迹;所求得的方程就是
点的运动的轨迹;所求得的方程就是 点的轨迹方程:点
点的轨迹方程:点 的轨迹方程就是指点
的轨迹方程就是指点 的坐标
的坐标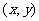 满足的关系式.本题的方法为求轨迹方程的一种基本方法,注意方法的归纳总结.
满足的关系式.本题的方法为求轨迹方程的一种基本方法,注意方法的归纳总结.
例3:某圆拱桥的示意图如右图,该圆拱的跨度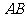 是
是 米,拱高
米,拱高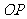 是
是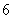 米,在建造时,每隔
米,在建造时,每隔 米需用一个支柱支撑,求支柱
米需用一个支柱支撑,求支柱 的长度(精确到
的长度(精确到 米).
米).
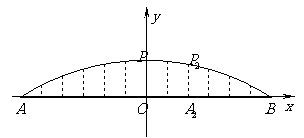 分析:若能够知道该圆拱所在的圆的方程,问题就变的很简单了,所以,我们联想到建立相应的直角坐标系,将问题转化为求圆的方程.
分析:若能够知道该圆拱所在的圆的方程,问题就变的很简单了,所以,我们联想到建立相应的直角坐标系,将问题转化为求圆的方程.
[解]以线段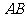 所在直线为
所在直线为 轴,线段
轴,线段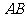 的中点
的中点 为坐标原点建立直角坐标系,那么点
为坐标原点建立直角坐标系,那么点 的坐标分别为
的坐标分别为
 ;
;
设圆拱所在的圆的方程为
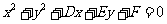 ,
,
∵点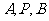 在所求的圆上,则坐标代入得:
在所求的圆上,则坐标代入得:
 ,解之得
,解之得 ,
,
∴圆拱所在的圆的方程为:
 ;
;
将点 的横坐标
的横坐标 代入圆方程,解得
代入圆方程,解得 (舍去负值).
(舍去负值).
答:支柱 的长约为
的长约为 米.
米.
点评:本题的关键利用图形建立直角坐标系,求出圆拱所在圆的方程,用代数的方法研究几何问题.
 追踪训练一
追踪训练一
3.形如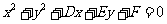 的都表
的都表
示圆吗?不是 .
(1)当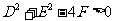 时,方程表
时,方程表
示以 为圆心,
为圆心,
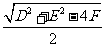 为半径的圆;
为半径的圆;
(2)当 时,方程表示一个点
时,方程表示一个点 ;
;
(3)当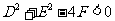 时,方程无实数解,即方程不表示任何图形;
时,方程无实数解,即方程不表示任何图形;
2.将 展开得:
展开得:
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com