
例5: 若过原点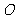 的直线
的直线 与连结
与连结 的线段相交,求直线
的线段相交,求直线 的倾斜角和斜率的取值范围.
的倾斜角和斜率的取值范围.
分析:结合图形可知,直线 介于直线
介于直线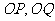 之间,即可得倾斜角范围;再根据倾斜角变化时,斜率变化规律可得斜率范围.
之间,即可得倾斜角范围;再根据倾斜角变化时,斜率变化规律可得斜率范围.
答案:倾斜角范围 ,斜率范围
,斜率范围 .
.
追踪训练二
1.已知 ,则直线
,则直线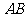 的倾斜角
的倾斜角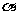 和斜率
和斜率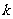 分别为(
分别为(  )
)


|
学生质疑 |
|
|
教师释疑 |
|
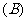





3.已知过点 ,
,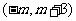 的直线
的直线 的斜率为
的斜率为 ,则实数
,则实数 的值为
的值为 .
.
|
学生质疑 |
|
|
教师释疑 |
|

2. 求证: 三点共线.
提示:∵
三点共线.
提示:∵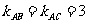 ,∴三点共线.
,∴三点共线.
例4:已知三点 在一条直线上,求实数
在一条直线上,求实数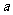 的值.
的值.
[解]由题意, ,
,
∴ ,∴
,∴ 或
或 .
.
点评:共线三点中任意两点确定的直线斜率相等.
思维点拔:
任何直线都有倾斜角和斜率吗?
根据直线倾斜角和斜率的概念,任何直线都有倾斜角.特别地,当直线与 轴平行或重合时,倾斜角为
轴平行或重合时,倾斜角为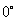 ;当直线与
;当直线与 轴垂直时,倾斜角为
轴垂直时,倾斜角为 ,此时直线斜率不存在.因此,除倾斜角为
,此时直线斜率不存在.因此,除倾斜角为 的直线外,其他直线都有斜率.
的直线外,其他直线都有斜率.
追踪训练
1. 的三个顶点
的三个顶点 ,
, ,写出
,写出 三边所在直线的斜率:
三边所在直线的斜率:
 ,
,
 ,
,
 .
.
1.直线的斜率:已知两点 ,如果
,如果 ,那么,直线
,那么,直线 的斜率为
的斜率为
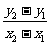 ;此时,斜率也可看成是
;此时,斜率也可看成是
 .
.
[精典范例]
 例1:如图,直线
例1:如图,直线 都经过点
都经过点 ,又
,又 分别经过点
分别经过点 ,
, ,试计算直线
,试计算直线 的斜率.
的斜率.
[解]设 的斜率分别为
的斜率分别为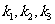 ,
,
则 ,
,
由图可知,
(1)当直线的斜率为正时,直线从左下方向右上方倾斜(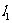 ),此时直线倾斜角为锐角;
),此时直线倾斜角为锐角;
 (2)当直线的斜率为负时,直线从左上方向右下方倾斜(
(2)当直线的斜率为负时,直线从左上方向右下方倾斜(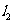 ),此时直线倾斜角为钝角;
),此时直线倾斜角为钝角;
(3)当直线的斜率为0时,直线与 轴平行或重合(
轴平行或重合(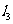 ),此时直线倾斜角为
),此时直线倾斜角为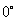 .
.
例2:已知直线 经过点
经过点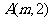 、
、 ,求直线
,求直线 的斜率.
的斜率.
[解]当 时,直线
时,直线 的斜率不存在,此时倾斜角为
的斜率不存在,此时倾斜角为 ;
;
当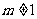 时,
时,
直线 的斜率
的斜率 .
.
点评:运用斜率公式求直线斜率时,一定要注意公式中 的条件.
的条件.
 例3:经过点
例3:经过点 画直线,使直线的斜率分别为:(1)
画直线,使直线的斜率分别为:(1) ;(2)
;(2) .
.
分析:根据两点确定一条直线,只需再确定直线上另一个点的位置.
[解](1)根据斜率 ,斜率为
,斜率为 表示直线上的任一点沿
表示直线上的任一点沿 轴方向向右平移4个单位,再沿
轴方向向右平移4个单位,再沿 轴方向向上平移3个单位后仍在此直线上,将点
轴方向向上平移3个单位后仍在此直线上,将点 沿
沿 轴方向向右平移4个单位,再沿
轴方向向右平移4个单位,再沿
 轴方向向上平移3个单位后得点
轴方向向上平移3个单位后得点 ,即可确定直线.
,即可确定直线.
(2)∵ ,
,
∴将点 沿
沿 轴方向向右平移5个单位,再沿
轴方向向右平移5个单位,再沿 轴方向向下平移4个单位后得点
轴方向向下平移4个单位后得点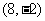 ,即可确定直线.
,即可确定直线.
[选修延伸]
2.掌握过两点的直线斜率的计算公式.
[课堂互动]
自学评价
重点:
直线的斜率和倾斜角的概念,过两点的直线的斜率的计算公式;直线的方程的几种形式,会根据已知条件选择恰当的形式表示直线;两点间的距离公式,点到直线的距离公式,会求两条平行线间的距离;根据斜率判定两直线的平行或垂直关系,会求两直线的交点坐标;
圆的标准方程与一般方程的概念,会根据条件选择恰当的形式求圆的方程;能根据给定直线与圆的方程,判断直线与圆、圆与圆的位置关系;
会用空间直角坐标系刻画点的位置,会用距离公式求空间两点间的距离.
难点:
几种形式的直线方程的推导;圆的标准方程的推导;直线与圆、圆与圆的位置关系中有关问题的探索.
第1课 直线的斜率(1)
[学习导航]
知识网络

学习要求
1.理解直线的斜率的概念;
例4: 讨论方程
 的几何意义.
的几何意义.
分析:类比空间两点的距离公式,构造点
[解]因为 ,
,
所以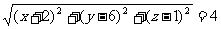
即动点 到定点
到定点 的距离等于4,
的距离等于4,
所以 .
.
表示动点 的轨迹:一个半径为4,球心为
的轨迹:一个半径为4,球心为 的球面
的球面
思维点拔:
注意类比方法在解决一些空间问题中的应用.
追踪训练二
1. 试解释方程
 的几何意义.
的几何意义.
答案:方程表示点 与点
与点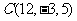 的距离为
的距离为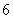 ,即点
,即点 在以点
在以点 为球心,半径为
为球心,半径为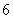 的球面上.
的球面上.
|
学生质疑 |
|
|
教师释疑 |
|
例4: 求点 关于
关于 平面,
平面, 平面及原点的对称点.
平面及原点的对称点.
[解]
 在
在 平面上的射影为
平面上的射影为 在
在 平面上的射影为
平面上的射影为 ,
,
 关于
关于 平面的对称点为
平面的对称点为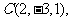 关于
关于 平面及原点的对称点分别为
平面及原点的对称点分别为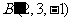 、
、
点评:一般的,点 关于
关于 平面的对称点为
平面的对称点为 ,关于
,关于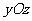 平面的对称点为
平面的对称点为 ,关于
,关于 平面的对称点为
平面的对称点为 ,关于原点的对称点
,关于原点的对称点
追踪训练二
1.写出分别在坐标轴、坐标平面上的点 的坐标所满足的条件.
的坐标所满足的条件.
2.已知一个圆经过直线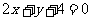 与圆
与圆 的两个交点,并且有最小面积,求此圆的方程.
的两个交点,并且有最小面积,求此圆的方程.
答案: .
.
|
学生质疑 |
|
|
教师释疑 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com