
3. 方程 表示( C
)
表示( C
)
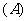 通过点
通过点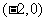 的所有直线
的所有直线
 通过点
通过点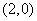 的所有直线
的所有直线
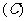 通过点
通过点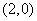 且不垂直于
且不垂直于 轴的直线
轴的直线
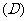 通过点
通过点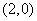 且除去
且除去 轴的直线
轴的直线
|
学生质疑 |
|
|
教师释疑 |
|

2.写出下列直线的斜截式方程:
(1)斜率是 ,在
,在 轴上的截距是
轴上的截距是 ;
;
(2)斜率是 ,与
,与 轴交点坐标为
轴交点坐标为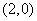 .
.
答案:(1) ;
;
(2) .
.
1. 写出下列直线的点斜式方程:
(1)经过点 ,斜率为
,斜率为 ;
;
(2)经过点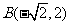 ,倾斜角为
,倾斜角为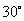 ;
;
(3)经过点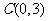 ,倾斜角是
,倾斜角是 ;
;
(4)经过点 ,倾斜角是
,倾斜角是 .
.
答案:(1)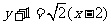 ;
;
(2)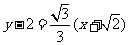 ;
;
(3) ;
;
(4) .
.
3.方程  叫做直线的斜截式方程,其中
叫做直线的斜截式方程,其中 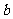 叫做直线在
叫做直线在  轴 上的截距.
轴 上的截距.
[精典范例]
例1:已知一条直线经过点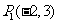 ,斜率为
,斜率为 ,求这条直线的方程.
,求这条直线的方程.
[解]∵直线经过点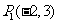 ,且斜率为
,且斜率为 ,
,
代入点斜式,得: ,
,
即 .
.
 点评:已知直线上一点的坐标和直线的斜率,可直接利用斜截式写出直线方程.
点评:已知直线上一点的坐标和直线的斜率,可直接利用斜截式写出直线方程.
例2:直线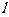 斜率为
斜率为 ,与
,与 轴的交点是
轴的交点是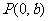 ,求直线
,求直线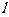 的方程.
的方程.
[解]代入直线的点斜式,得: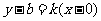 ,即
,即 .
.
点评:
(1)直线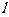 与
与 轴交点
轴交点 ,与
,与 轴交点
轴交点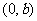 ,称
,称 为直线
为直线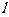 在
在 轴上的截距,称
轴上的截距,称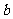 为直线
为直线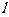 在
在 轴上的截距(截距可以大于
轴上的截距(截距可以大于 ,也可以等于或小于
,也可以等于或小于 );
);
(2)方程由直线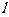 斜率
斜率 和它在
和它在 轴上的截距
轴上的截距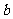 确定,叫做直线方程的斜截式.
确定,叫做直线方程的斜截式.
例3:(1)求直线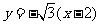 的倾斜角;
的倾斜角;
(2)求直线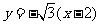 绕点
绕点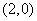 按顺时针方向旋转
按顺时针方向旋转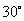 所得的直线方程.
所得的直线方程.
[解](1)设直线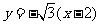 的倾斜角为
的倾斜角为 ,则
,则 ,又∵
,又∵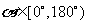 , ∴
, ∴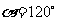 ;
;
(2)∴所求的直线的倾斜角为 ,且经过点
,且经过点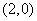 ,
,
所以,所求的直线方程为 .
.
例4:在同一坐标作出下列两组直线 ,分别说出这两组直线有什么共同特征?
(1) ,
, ,
, ,
,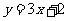 ,
, ;
;
(2) ,
, ,
, ,
, ,
,
[解]图略;(1)这些直线在 轴上的截距都为
轴上的截距都为 ,它们的图象经过同一点
,它们的图象经过同一点 ;
;
(2)这些直线的斜率都为 ,它们的图象平行.
,它们的图象平行.
追踪训练
2.直线 经过点
经过点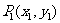 ,当直线斜率不存在时,直线方程为
,当直线斜率不存在时,直线方程为  ;当斜率为
;当斜率为 时,直线方程为
时,直线方程为 ,该方程叫做直线的点斜式方程.
,该方程叫做直线的点斜式方程.
1.求直线的方程,其实就是研究直线上任意一点 的 坐标
的 坐标 和
和 之间的关系.
之间的关系.
3.掌握斜率不存在时的直线方程,即 .
[课堂互动]
.
[课堂互动]
自学评价
2.能通过待定系数(直线上的一个点的坐标 及斜率
及斜率 ,或者直线的斜率
,或者直线的斜率 及在
及在 轴上的截距
轴上的截距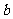 )求直线方程;
)求直线方程;
1.掌握由一点和斜率导出直线方程的方法,掌握直线的点斜式方程;了解直线方程的斜截式是点斜式的特例;
2.设点 ,直线
,直线 过点
过点 ,且与线段
,且与线段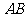 相交,求直线
相交,求直线 的斜率的取值范围.
的斜率的取值范围.
答案:由直线 过点
过点 ,且与线段
,且与线段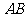 相交可得:直线
相交可得:直线 的斜率的变化可以看作是以
的斜率的变化可以看作是以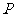 为旋转中心,直线
为旋转中心,直线 逆时针旋转到直线
逆时针旋转到直线 的过程中斜率的变化,又∵
的过程中斜率的变化,又∵ ,
, ,结合图形(图略)可得:直线
,结合图形(图略)可得:直线 的斜率的取值范围是
的斜率的取值范围是 或
或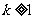 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com