
2. 直线 和
和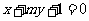 平行的条件是 (
平行的条件是 (
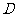 )
)

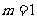
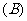




 或
或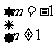
1.若过两点 和
和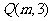 的直线与直线
的直线与直线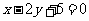 平行,则
平行,则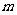 的值为(
的值为(  )
)
 5
5  4
4  9
9  0
0
2.已知两直线的位置关系,求字母系数值的方法(注意:要对直线斜率不存在的情况进行讨论).
例4:求过点 ,且与直线
,且与直线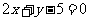 平行的直线方程.
平行的直线方程.
分析:抓住题目中的有效信息,直线平行则斜率相等,然后结合点 ,利用点斜式便能求出直线方程.
,利用点斜式便能求出直线方程.
[解]已知直线的斜率 ,
,
∵两直线平行,∴所求直线的斜率也为 ,
,
所以,所求直线的方程为: ,即
,即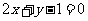 .
.
另解:设与直线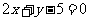 平行的直线
平行的直线 的方程为:
的方程为: ,
,
 过点
过点 ,∴
,∴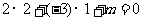 ,解之得
,解之得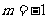 ,
,
所以,所求直线的方程为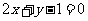 .
.
点评:(1)一般地与直线 平行的直线方程可设为
平行的直线方程可设为 ,其中
,其中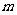 待定;
待定;
(2)把上题改为求与直线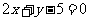 平行,且在两坐标轴上的截距之和为
平行,且在两坐标轴上的截距之和为 的直线
的直线 的方程.(
的方程.(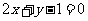 )
)
追踪训练一
2.通过分类讨论、数形结合等数学思想的应用,培养学生思维的严谨性和辨证性.
[课堂互动]
自学评价
判定直线 与
与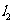 平行的前提是:
平行的前提是:
是不重合的两条直线;
如果 、
、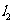 斜率都存在,则直线平行能得到斜率相等,反之,斜率相等也能得到直线平行;
斜率都存在,则直线平行能得到斜率相等,反之,斜率相等也能得到直线平行;
如果 、
、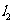 斜率都不存在,那么两直线都垂直于
斜率都不存在,那么两直线都垂直于 轴,故它们 平行 .
轴,故它们 平行 .
[精典范例]
例1:已知直线方程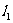 :
:
 :
: ,证明:
,证明: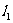 //
// .
.
分析:在两条直线斜率都存在的情况下,若要证明两直线平行,即证斜率相等.
[证明]把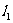 和
和 的方程写成斜截式
的方程写成斜截式
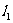 :
: ,
,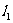 :
: ,
,
∵ ,
, ,
, ∴
∴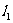 //
// .
.
点评:(1)判定两直线平行的条件是直线的斜率和截矩,因此,要把方程化为斜截式;
(2)判定两直线平行,首先判断斜率相等,若两直线斜率相等,则两直线可能平行也可能重合,还需再进一步判断截距不相等;
如果两条直线斜率不存在,两条直线为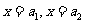 ,只需
,只需 即可.
即可.
(3)判定两直线重合,首先判断两条直线斜率相等,再判定截距相等.如果两条直线斜率都不存在,两直线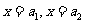 ,只需
,只需 即可.
即可.
例2:求证:顺次连结 四点所得的四边形是梯形.
四点所得的四边形是梯形.
分析:判断一个四边形是梯形,不仅要判断一组对边平行,还要判断另一组对边不平行.
[证明]∵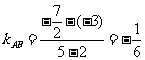 ,
,
 ,∴
,∴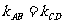 ,
,
从而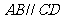 .
.
又∵ ,
,
 ,∴
,∴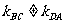 ,
,
从而直线 与
与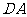 不平行,
不平行,
∴四边形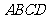 是梯形.
是梯形.
点评:在判断哪组对边平行时,不妨先在坐标系中将各点画出,结合图形作判断,再进行证明.
例3:(1)两直线 和
和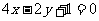 的位置关系是 平行或重合.
的位置关系是 平行或重合.
(2)若直线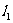 :
: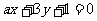 与
与 :
: 互相平行,则
互相平行,则 的值为
的值为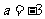 .
.
分析:(1)若两直线斜率不等,必定相交;若两直线斜率相等,则平行或重合;
(2)在两直线斜率存在的前提下,若两直线平行,则斜率相等,可以此来求直线方程中的字母系数.
[解](2)①当 时,
时,

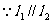 ,∴
,∴ ,∴
,∴ ,
,
即 ,解得
,解得 或
或 ,
,
当 两方程化为
两方程化为 与
与 显然平行,
显然平行,
当 两方程化为
两方程化为 与
与 两直线重合,
两直线重合,
∴ 不符合,
不符合,
②当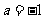 时,两直线不平行,
时,两直线不平行,
∴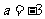 .
.
点评: 1.已知两直线的方程,判断它们位置关系的方法;
1.掌握用斜率判定两条直线平行的方法,并会根据直线方程判断两条直线是否平行;
3.证明:不论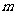 取什么实数,直线
取什么实数,直线
 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.
提示:仿“例6”可证得直线过定点 .
.
|
学生质疑 |
|
|
教师释疑 |
|
2.若直线 经过第一、二、三象限,求实数
经过第一、二、三象限,求实数 满足的条件.
满足的条件.
答案:将直线方程化为: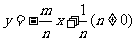 ,由已知可得
,由已知可得 ;
;
当 时,直线方程为
时,直线方程为 ,不满足条件,
,不满足条件,
∴实数 满足条件
满足条件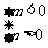
例6:求证:不论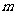 取什么实数,直线
取什么实数,直线
 恒过定点,并求此定点坐标.
恒过定点,并求此定点坐标.
[解]法1:令 得
得 ;令
;令 得
得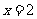 ;两直线交点为
;两直线交点为 ,将点
,将点 坐标代入原直线方程,得
坐标代入原直线方程,得
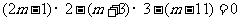 恒成立,因此,直线过定点
恒成立,因此,直线过定点 .
.
法2:将方程化为
 ,
,
当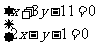 即
即 时,以上方程恒成立,即定点
时,以上方程恒成立,即定点 的坐标恒满足原直线方程,因此,直线过定点
的坐标恒满足原直线方程,因此,直线过定点 .
.
例7:在例5中,能证明“直线恒过第三象限”吗?
提示:直线恒过定点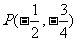 ,而
,而 点在第三象限.
点在第三象限.
思维点拔:
证明直线过定点问题,要找到一定点,证明其坐标始终满足直线方程即可,通常采用“例6”中的两种方法来寻求定点.
 追踪训练二
追踪训练二
1.若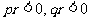 ,则直线
,则直线 不经过(
不经过(  )
)
 第一象限
第一象限  第二象限
第二象限
 第三象限
第三象限  第四象限
第四象限
例5: 若直线 不经过第二象限,求
不经过第二象限,求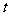 的取值范围.
的取值范围.
分析:可以从直线的斜率和直线在 轴上的截距两方面来考虑.
轴上的截距两方面来考虑.
[解]直线方程可化为:
 ,
,
由题意得: ,解得
,解得 .
.
例3:求经过点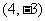 且在两坐标轴上的截距绝对值相等的直线方程.
且在两坐标轴上的截距绝对值相等的直线方程.
分析: 涉及直线在坐标轴上的截距时,可选择直线方程的截距式.
[解]设直线在 轴与
轴与 轴上的截距分别为
轴上的截距分别为 ,①当
,①当 时,设直线方程为
时,设直线方程为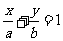 ,
,
∵直线经过点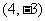 ,∴
,∴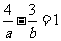 ,
,
∵ ,∴
,∴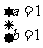 或
或 ,∴直线方程为
,∴直线方程为  或
或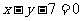 ;
;
②当 时,则直线经过原点及
时,则直线经过原点及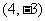 ,
,
∴直线方程为  ,
,
综上,所求直线方程为 或
或 或
或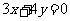 .
.
点评:题设中涉及到了直线在两坐标轴上的截距,因此可考虑用截距式,但应注意到截距能否为零,这是应用截距式求直线方程最易出错和疏忽的地方.
例4:直线 与两坐标轴在第一象限围成的三角形面积为2,两截距之差为3,求直线
与两坐标轴在第一象限围成的三角形面积为2,两截距之差为3,求直线 的方程.
的方程.
分析:根据题意,直线 在两坐标轴上截距都大于零,因此可以用截距式方程.
在两坐标轴上截距都大于零,因此可以用截距式方程.
[解]由题意,直线 在两坐标轴上截距都大于零,
在两坐标轴上截距都大于零,
故可设直线方程为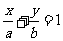
 ,
,
由已知得: ,
,
解得 或
或
或 (舍)或
(舍)或 (舍)
(舍)
∴直线方程为 或
或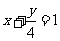 .
.
思维点拔:
过两点 的直线能写成两点式的条件是
的直线能写成两点式的条件是 且
且 ,如果没有这个条件,就必须分类讨论,这点容易被忽略;只有当直线在坐标轴上的截距都不为零时,才可以用直线方程的截距式.
,如果没有这个条件,就必须分类讨论,这点容易被忽略;只有当直线在坐标轴上的截距都不为零时,才可以用直线方程的截距式.
追踪训练二
1.求过点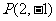 ,在
,在 轴和
轴和 轴上的截距分别为
轴上的截距分别为 ,且满足
,且满足 的直线方程.
的直线方程.
答案:分截距为零、不为零两种情况讨论,可得所求直线方程为 或
或 .
.
|
学生质疑 |
|
|
教师释疑 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com