
3. 过原点作直线 的垂线,若垂足为
的垂线,若垂足为 ,则直线
,则直线 的方程是
的方程是 .
.
2.(2000京皖春,6)直线( )x+y=3和直线x+(
)x+y=3和直线x+( )y=2的位置关系是
(
)y=2的位置关系是
(  )
)
( )相交不垂直 (
)相交不垂直 ( )垂直
)垂直
(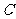 )平行 (
)平行 ( )重合
)重合
1. 以 为顶点的三角形是
(
为顶点的三角形是
( )
)
( )锐角三角形 (
)锐角三角形 ( )直角三角形 (
)直角三角形 (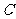 )钝角三角形
)钝角三角形
2.理解两条直线垂直条件的推导过程,注意解几思想的渗透和表述的规范性,培养学生的探索和概括能力.
[课堂互动]
自学评价
(1)当两条直线的斜率都存在时,如果它们 互相垂直 ,那么它们的斜率的乘积等于 ,反之,如果它们的斜率的乘积等于
,反之,如果它们的斜率的乘积等于 ,那么它们 互相垂直 .
,那么它们 互相垂直 .
(2)若两条直线 中的一条斜率不存在,则另一条斜率为
中的一条斜率不存在,则另一条斜率为  时,
时,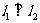 .
.
[精典范例]
例1:(1)已知四点
 ,求证:
,求证: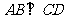 .
.
(2)已知直线 的斜率为
的斜率为 ,直线
,直线 经过点
经过点 ,且
,且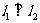 ,求实数
,求实数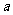 的值.
的值.
[证明](1)由斜率公式得: ,
,
则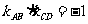 , ∴
, ∴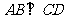 .
.
(2)∵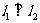 ,∴
,∴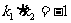 ,
,
即 ,
,
解得 或
或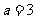 ,
,
∴当 或
或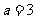 时,
时,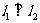 .
.
点评:本题是两直线垂直判定的简单应用.
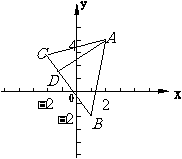 例2:已知三角形的三个顶点为
例2:已知三角形的三个顶点为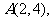

 ,求
,求 边上的高
边上的高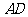 所在的直线方程.
所在的直线方程.
分析:由 和
和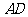 垂直,求出
垂直,求出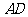 的斜率,利用直线的点斜式便可求出高
的斜率,利用直线的点斜式便可求出高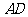 所在的直线方程.
所在的直线方程.
[解]直线 的斜率为
的斜率为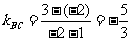 , ∵
, ∵ , ∴
, ∴ ,
,
根据点斜式,得到所求直线的方程为
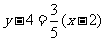 , 即
, 即 .
.
点评:一般地,与直线 垂直的直线的方程可设为
垂直的直线的方程可设为 ,其中
,其中 待定.
待定.
例3:在路边安装路灯,路宽23 ,灯杆长
,灯杆长 ,且与灯柱成
,且与灯柱成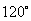 角,路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高
角,路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高 为多少米时,灯罩轴线正好通过道路路面的中线?(精确到
为多少米时,灯罩轴线正好通过道路路面的中线?(精确到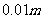 )
)
[解]记灯柱顶端为 ,灯罩顶为
,灯罩顶为 ,灯管为
,灯管为 ,灯罩轴线与道路中线交于点
,灯罩轴线与道路中线交于点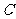 .以灯柱底端
.以灯柱底端 为原点,灯柱
为原点,灯柱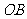 为
为 轴,建立如图所示的直角坐标系.
轴,建立如图所示的直角坐标系.
点 的坐标为
的坐标为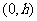 ,点
,点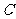 的坐标为
的坐标为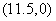 ,
,
∵ ,∴直线
,∴直线 的倾斜角为
的倾斜角为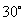 ,
,
则点 的坐标为(
的坐标为( ),
),
即(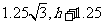 ),
),
∴
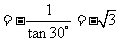 ,由直线的点斜式方程,得
,由直线的点斜式方程,得 的方程为
的方程为 ,
,
 灯罩轴线
灯罩轴线 过点
过点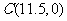 ,
,
∴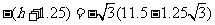 ,
,
解得 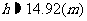
答:灯柱高 约为
约为
 .
.
点评:读懂题意,画出示意图,建立直角坐标系,构造数学模型是关键.
追踪训练一
1.掌握两条直线垂直的判定方法,并会根据直线方程判断两条直线是否垂直;
3.求与直线 平行,并且和两坐标轴在第一象限所围成的三角形面积是24的直线方程.
平行,并且和两坐标轴在第一象限所围成的三角形面积是24的直线方程.
[解]∵直线 的斜率为
的斜率为 ,
,
∴设所求直线方程为 ,
,
令 ,得
,得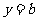 ;令
;令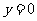 ,得
,得 ,
,
由题意,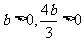 ,∴
,∴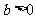 ,
,
∴ ,∴
,∴ ,
,
故所求直线方程为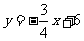 ,即
,即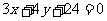 .
.
点评:直线方程为 可化为
可化为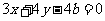 ,令
,令 ,即可得
,即可得 .因此,与
.因此,与 平行的直线也可设为
平行的直线也可设为 ,但注意到两直线不重合,所以
,但注意到两直线不重合,所以 .
.
|
学生质疑 |
|
|
教师释疑 |
|
2.与直线 平行且在两坐标轴上截距之和为
平行且在两坐标轴上截距之和为 的直线
的直线 的方程为
的方程为 .
.
1.若直线mx+4y-1=0与直线x+my-3=0不平行,求实数m的取值范围是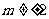 .
.
4. 若直线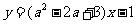 与直线
与直线 平行,则
平行,则 的值为
的值为 .
.
思维点拔:
课本中是在两条直线的斜率都存在的前提下,得出两直线平行的等价条件的.在具体解题时,应注意考虑直线斜率不存在的情形(如例3(2)、追踪训练一第2题).另外,在判定两直线平行时,还要注意出现两直线重合的情况.
追踪训练二
3. 平行于直线 ,且在
,且在 轴上截距为
轴上截距为 的直线方程是
的直线方程是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com