
3.学生通过一般形式的直线方程解的讨论,加深对解析法的理解,培养转化能力.
[课堂互动]
自学评价
(1)求两直线的交点坐标只需将这两条直线的方程联立成方程组, 方程组的解 即为交点坐标.
(2)在解由两直线的方程组成的方程组的时候可能出现的三种结果是:
①方程组有一组解,该解为 交点坐标 ;
②方程组有无数组解,此时两直线的位置关系为 重合 ,交点个数为 无数个 ;
③方程组无解,此时两直线的位置关系是 平行 ,交点个数为 0个.
[精典范例]
例1:分别判断下列直线是否相交,若相交,求出它们的交点:
(1) :
: ,
, :
: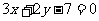 ;
;
(2) :
: ,
,
 :
: ;
;
(3) :
: ,
, :
: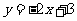 .
.
[解](1)因为方程组 的解为
的解为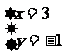 ,
,
因此直线 相交,交点坐标为
相交,交点坐标为 .
.
(2)方程组 有无数组解,
有无数组解,
这表明直线 重合.
重合.
(3)方程组 无解,
无解,
这表明直线 没有公共点,故
没有公共点,故 ∥
∥ .
.
点评: 研究两条直线 的位置关系(相交、重合、平行)可以转化为两条直线方程所得的方程组
的位置关系(相交、重合、平行)可以转化为两条直线方程所得的方程组 的解的个数问题.
的解的个数问题.
例2:直线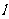 经过原点,且经过另外两条直线
经过原点,且经过另外两条直线 ,
, 的交点,求直线
的交点,求直线 的方程.
的方程.
分析:法一 由两直线方程组成方程组 ,求出交点
,求出交点 ,再过原点
,再过原点 ,由两点求直线方程.
,由两点求直线方程.
法二 设经过两条直线 ,
, 交点的直线方程为
交点的直线方程为 ,又过原点,由
,又过原点,由 代入可求
代入可求 的值.
的值.
点评:已知直线 :
: ,
, :
: 相交,那么过两直线的交点的直线方程可设为
相交,那么过两直线的交点的直线方程可设为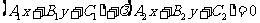

例3:某商品的市场需求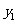 (万件)、市场供求量
(万件)、市场供求量 (万件)、市场价格
(万件)、市场价格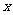 (元/件)分别近似地满足下列关系:
(元/件)分别近似地满足下列关系: .当
.当 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求市场平衡价格和平衡需求量;
(2)若要使平衡需求量增加4万件,政府对每件商品应给予多少元补贴?
分析:市场平衡价格和平衡需求量实际上就是两直线 交点的横坐标和纵坐标,即方程组
交点的横坐标和纵坐标,即方程组 的解.
的解.
[解](1)解方程组 得
得 ,
,
故平衡价格为30元/件,平衡需求量为40元/件.
(2)设政府给予 元/件补贴,此时的市场平衡价格(即消费者支付价格)
元/件补贴,此时的市场平衡价格(即消费者支付价格)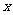 元/件,则供货者实际每件得到
元/件,则供货者实际每件得到 元.依题意得方程组
元.依题意得方程组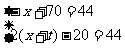 ,解得
,解得 .
.
因此,政府对每件商品应给予6元补贴.
点评:这是一道关于两直线交点的实际应用题,关键要读懂题目意思,而后通过解方程组解决问题.
追踪训练一
2.当两条直线相交时,会求交点坐标;
1.知道两条直线的相交、平行和重合三种位置关系,对应于相应的二元一次方程组有唯一解、无解和无穷多组解;
4.分别经过点A(1,2)、B(2,4)的两条直线互相平行,当它们之间的距离达到最大时,求这两条直线的方程.
答案:经过 的直线分别是
的直线分别是 及
及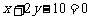 .
.
|
学生质疑 |
|
|
教师释疑 |
|
3.过点 的所有直线中,距离原点最远的直线方程是
的所有直线中,距离原点最远的直线方程是 .
.
2.由四条直线: ,
, ,
,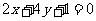 ,
, 围成的四边形是
(
围成的四边形是
(  )
)
 等腰梯形
等腰梯形 梯形
梯形  长方形
长方形 正方形
正方形
1.若直线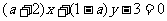 与
与 互相垂直,则实数
互相垂直,则实数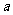 的值为
的值为 .
.
2.在解有关两直线平行或垂直问题时,应注意它们的斜率是否存在,否则需分类讨论.
追踪训练二
1.求直线方程时,与 或
或 平行的直线可分别设为
平行的直线可分别设为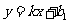 或
或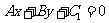 (其中
(其中 为待定系数);与
为待定系数);与 或
或 垂直的直线可分别设为
垂直的直线可分别设为 或
或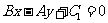 (其中
(其中 为待定系数).
为待定系数).
4. 已知两直线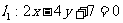 ,
, ,求证:
,求证: .
.
[选修延伸]
例4:(课本第91页 习题
第12题)直线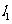 和
和 的方程分别是
的方程分别是 和
和 ,其中
,其中 不全为0,
不全为0, 也不全为0,试探究:
也不全为0,试探究:
(1)当 时,直线方程中的系数应满足什么关系?
时,直线方程中的系数应满足什么关系?
(2)当 时,直线方程中的系数应满足什么关系?
时,直线方程中的系数应满足什么关系?
分析:由于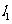 和
和 的斜率可能不存在,因此分类讨论.
的斜率可能不存在,因此分类讨论.
[解](1)①当两直线方程中 的系数有一个为0时,
的系数有一个为0时,
不妨设 ,则必有
,则必有 ,此时直线
,此时直线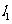 垂直于
垂直于 轴,其方程为
轴,其方程为 ,由
,由 知
知 也垂直于
也垂直于 轴,其方程可以为
轴,其方程可以为 ,
,
此时满足 ;反之也成立.
;反之也成立.
②当两直线方程中 的系数均不为0时,
的系数均不为0时,
直线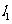 和
和 的斜率分别为
的斜率分别为 ,
, ,由
,由 得
得 ,
,
即 .反之也成立.
.反之也成立.
综合①②可知:当 时,
时, .
.
(2)①当两直线方程中 的系数有一个为0时,
的系数有一个为0时,
不妨设 ,则必有
,则必有 ,此时直线
,此时直线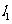 垂直于
垂直于 轴,其方程为
轴,其方程为 ,由
,由 知,直线
知,直线 平行于
平行于 轴,故其方程为
轴,故其方程为 ,
,
满足, ;反之也成立.
;反之也成立.
②当两直线方程中 的系数均不为0时,
的系数均不为0时,
直线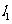 和
和 的斜率分别为
的斜率分别为 ,
, ,
,
由 知,
知, ,∴
,∴ .反之也成立.
.反之也成立.
综合①②可知:当 时,
时, .
.
点评:斜率是否存在的讨论是本题的难点所在.另外,分类讨论的数学思想也得到了充分的体现.
思维点拔:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com