7、本章主要思想方法：数形结合，分类讨论，函数与方程，等价变换等。

6、对称是平面几何的基本变换。在掌握点关于点及直线对称的基础上，理解曲线与曲线之间的中心对称及轴对称。善于利用对称的知识解题。

5、圆与二元二次方程一一对应，这些二元二次方程方程特征为：(1)二次项中无xy交叉项；(2)x²，y²项前面系数相等；(3)x，y的一次项系数D，E及常数项F满足D²+E²-4F>0。

圆方程常见形式：(1)标准式：(x-a)²+(y-b)²=R²(R>0)，其中(a，b)为圆心，R为半径；(2)一般式：x²+y²+Dx+Ey+F=0；(3)参数式：(x-a)²+(y-b)²=R²(R>0)的参数式为：x=a+Rcosθ，y=b+Rsinθ，其中θ为参数，表示旋转角，参数式常用来表示圆周上的点。

求圆方程的原理与求直线方程完全类似。

直线和圆位置关系及圆和圆位置关系常借助于平面几何知识，而不采用方程组理论(△法)。

4、当直线位置不确定时，直线对应的方程中含有参数。含参数方程中有两种特殊情形，它们的对应的直线是有规律的，即旋转直线系和平行直线系。

在点斜式方程y-y₀=k(x-x₀)中，当(x₀，y₀)确定，k变化时，该方程表示过定点(x₀，y₀)的旋转直线系，当k确定，(x₀，y₀)变化时，该方程表示平行直线系。

这些直线系还有其它表示形式：

(1)已知直线l：Ax+By+C=0，则

方程Ax+By+m=0(m为参数)表示与l平行的直线系；方程-Bx+Ay+n=0(n为参数)表示与l垂直的直线系。

　 (2)已知直线l₁：A₁x+B₁y+C₌₁=0，直线l₂：A₂x+B₂y+C₂=0，则方程A₁x+B₁y+C₁+λ(A₂x+B₂y+C₂)=0表示过l₁与l₂交点的直线系(不含l₂)

掌握含参数方程的几何意义是某种直线系，不仅可以加深数形结合的思想，还可以优化解题思想。

3、直线是平面几何的基本图形，它与方程中的二元一次方程Ax+By+C=0(A²+B²≠0)一一对应。

从几何条件看，已知直线上一点及直线方向与已知直线上两点均可确定直线；从对应方程看，直线方程两种典型形式：点斜式(斜截式)，两点式(截距式)，因此求直线方程，常用待定系数法。即根据题意，选择方程的适当形式；由已知条件，列关于参数的方程(组)。

当点P(x₀，y₀)在直线Ax+By+C=0上时，其坐标满足方程Ax₀+By₀+C=0；当P不在直线Ax+By+C=0上时，Ax₀+By₀+C≠0，即Ax₀+By₀+C>0或Ax₀+By₀+C<0。这就是二元一次不等式的几何意义：二元一次不等式Ax+By+C>0(或<0)表示直线Ax+By+C=0上方或下方区域，其具体位置的确定常用原点(0，0)代入检验。利用此几何意义，可以解决一类二元函数的最值问题。这就是线性规划的内容。

因直线与二元一次方程Ax+By+C=0(A²+B²≠0)一一对应，即由有序数组(A，B，C)确定，因此研究直线与直线之间的位置关系就是考察直线对应的数组间关系。

设直线l₁：A₁x+B₁y+C₁=0(A₁²+B₁²≠0)，直线l₂：A₂x+B₂y+C₂=0(A₂²+B₂²≠0)

则：l₁∥l₂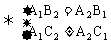

l₁与l₂相交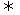A₁B₂≠A₂B₁

其夹角公式为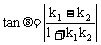，其中k₁，k₂分别表示l₁及l₂斜率，当l₁或l₂斜率不存在时，画图通过三角形求解，l₁与l₂夹角为θ∈(0，]

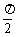特例：l₁⊥l₂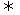A₁A₂+B₁B₂=0(此时不能用夹角公式求解)

利用点P(x₀，y₀)到直线l：Ax+By+C=0的距离公式d=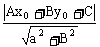可以求出两平行直线：Ax+By+C₁=0，Ax+By+C₂=0(C₁≠C₂)间的距离d=。

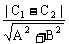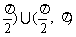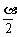2、直线的倾斜角α和斜率k是描述直线位置的重要参数，它们之间关系是正切函数关系：k=tanα，α∈[0，，当α=时，直线斜率不存在，否则由α求出唯一的k与之对应。

当已知k，求倾斜角α时：k≥0时，α=arctank；k<0时，α=π+arctank。或：k=0时，α=0；k≠0时，cotα=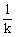,α=arccot。

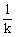由正切函数可知，当α∈(0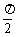，)，α递增时，斜率k→+∞。当α∈(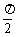，π)，α递减时，斜率k→-∞。

当涉及到斜率参数时，通常对k是否存在分类讨论。

1、　 曲线和方程是中学数学的两种常见研究对象。借助于平面直角坐标系，形和数可以得到高度的统一，它们最基本的对应关系是点和有序数对的一一对应。当点运动形成轨迹时，对应坐标便会满足一个方程。当曲线C和方程F(x，y)=0满足如下关系时：①曲线C上点的坐标都是方程F(x，y)=0的解；②以方程F(x，y)=0的解为坐标的点都在曲线C上，则称曲线C为方程F(x，y)=0表示的曲线；方程F(x，y)=0是曲线C表示的方程。从集合角度看，点集(曲线)与方程解集相等。解析几何研究的内容就是给定曲线C，如何求出它所对应的方程，并根据方程的理论研究曲线的几何性质。其特征是以数解形。坐标法是几何问题代数化的重要方法。

3、直线和圆位置关系的研究。

2、圆的方程三种形式，如何求圆的方程。

1、直线方程的五种表现形式，如何求直线方程；二元一次不等式的几何意义及运用。