
2、在边长为1的正方形网格中,有形如帆船的图案①和半径为2的⊙P。
⑴将图案①进行平移,使A点平移到点E,画出平移后的图案;
⑵以点M为位似中心,在网格中将图案①放大2倍,画出放大后的图案,并在放大后的图案中标出线段AB的对应线段CD;
⑶在⑵所画的图案中,线段CD被⊙P所截得的弦长为 。(结果保留根号)

解:⑴平移后的图案,如图所示;⑵放大后的图案,如图所示;

 ⑶线段CD被⊙P所截得的弦长为
⑶线段CD被⊙P所截得的弦长为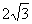 。
。
1、如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)。
(1)画出“基本图形”关于原点O对称的四边形A1B1C1D1,并求出A1,B1,C1,D1的坐标.
A1( , ),B1( , ),C1( , ),D1( , ) ;
(2)画出“基本图形”关于x轴的对称图形A2B2C2D2 ;
(3)画出四边形A3B3C3D3,使之与前面三个图形组成的图形既是中心对称图形又是轴对称图形。

解:(1)A1(-4,-4 ),B1(-1,-3),
 C1(-3,-3),D1(-3,-1) .
C1(-3,-3),D1(-3,-1) .
正确画出四边形A1B1C1D1
(2)正确画出图形A2B2C2D2
(3)正确画出图形A3B3C3D3
21.(1)依题意: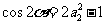 ,则
,则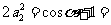 ,
,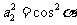 ;
;
而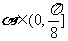 ,又
,又 ,所以
,所以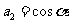 ,
………………1分
,
………………1分
同样可求得 ;
………………2分
;
………………2分
(2)猜测 ,
,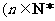 ).
………………4分
).
………………4分
①用数学归纳法证明:显然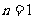 时猜想正确 ;
………………5分
时猜想正确 ;
………………5分
②假设 时猜想成立,即
时猜想成立,即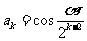 ,
,
则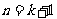 时,∵
时,∵ ,∴
,∴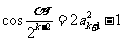 ,即
,即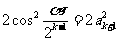 ,而
,而 ,
,
故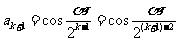 ,
………………6分
,
………………6分
这就是说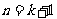 猜想也成立,故对任意正整数
猜想也成立,故对任意正整数 都有
都有 .
………………7分
.
………………7分
(3) .
………………9分
.
………………9分
证明: 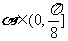 ,
,
则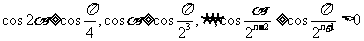 ,
………10分
,
………10分
则
 ,
,
∴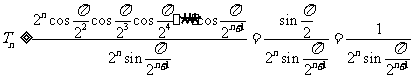 ;
………11分
;
………11分
设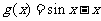 ,
, ,则
,则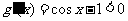 ,
,
即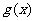 为
为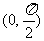 上的减函数,∴
上的减函数,∴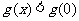 ,故
,故 时,
时,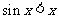 , ………12分
, ………12分
而 ,∴
,∴ ,
,
∴ ,
………13分
,
………13分
∴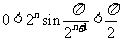 ,
,
则 ,即
,即 .
………14分
.
………14分
20.解:(1)设椭圆C的方程为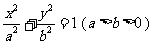 ,
………1分
,
………1分
抛物线方程化为 ,其焦点为
,其焦点为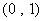 ,
,
椭圆C的一个顶点为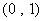 ,即
,即 ,
………3分
,
………3分
由 ,得
,得 ,
………5分
,
………5分
∴椭圆C的方程为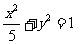 .
……………6分
.
……………6分
(2)由(1)得 ,
………………………7分
,
………………………7分
设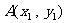
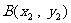 ,
,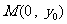 ,显然直线
,显然直线 的斜率存在,
的斜率存在,
设直线 的方程为
的方程为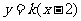 ,
…………………8分
,
…………………8分
代入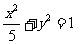 ,并整理得
,并整理得
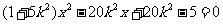 ,
………………9分
,
………………9分
∴ .
…………………10分
.
…………………10分
又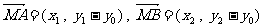 ,
,
 ,
,
由 ,
, ,得
,得
 ,
,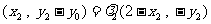 ,
,
∴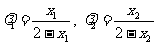 , ……………………12分
, ……………………12分
∴ .
………………14分
.
………………14分
19. 解:(1)当 ,
, ,即
,即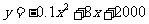 , 3分
, 3分
当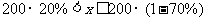 时,
时,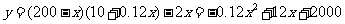 , 6分
, 6分
所以 与
与 的函数关系式为
的函数关系式为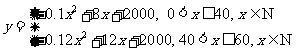 ;
8分
;
8分
(2)由 ,
,
而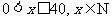 ,则
,则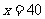 时,
时,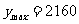 ;
10分
;
10分
由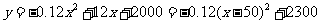 ,
,
而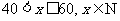 ,则
,则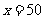 时,
时, ;
12分
;
12分
由于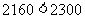 ,则当
,则当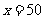 时,公司获利最大.
13分
时,公司获利最大.
13分
答:裁员50人时,公司获得最大的经济效益. 14分
18.(1)证明:连结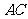 ,在
,在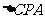 中
中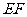 //
// ,
……2分
,
……2分
且
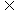 平面
平面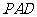 ,
, 平面
平面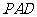 ,
,

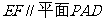 .…………………………………………………………………………………………………….4分
.…………………………………………………………………………………………………….4分
(2)证明:因为面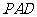
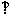 面
面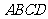 、平面
、平面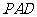
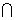 面
面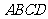
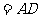 、
、 ,
,
所以,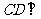 平面
平面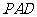 ,
,  .………………………………………………………………………6分
.………………………………………………………………………6分
又 ,所以
,所以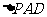 是等腰直角三角形,且
是等腰直角三角形,且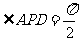 ,
,
即 ;…………………………………………………………………………………………………………………….8分
;…………………………………………………………………………………………………………………….8分
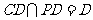 ,且
,且 、
、
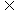 面
面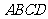 ,
,

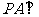 面
面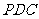 ;
;
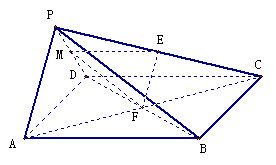 又
又 面
面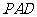 ,面
,面 面
面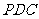 .……………………………………………………………..10分
.……………………………………………………………..10分
(3)解:设 的中点为
的中点为 ,连结
,连结 ,
,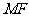 ,则
,则 ;
;
由(Ⅱ)知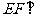 面
面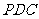 ,
, 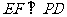 ,
,
 面
面 ,
, ,
,
 是二面角
是二面角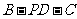 的平面角;……………………………………….12分
的平面角;……………………………………….12分
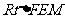 中,
中,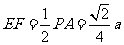 ,
,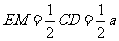 ,
,
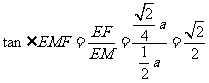 ,故所求二面角的正切为
,故所求二面角的正切为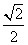 .……14分
.……14分
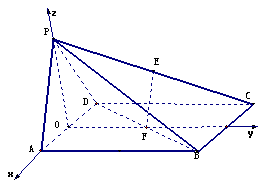 另解:如图,取
另解:如图,取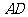 的中点
的中点 , 连结
, 连结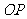 ,
,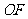 .
.
∵ , ∴
, ∴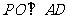 .
.
∵侧面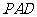
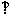 底面
底面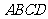 ,
,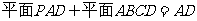 ,
,
∴ ,
,
而 分别为
分别为 的中点,∴
的中点,∴ ,又
,又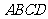 是正方形,故
是正方形,故 .
.
∵ ,∴
,∴ ,
,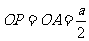 .
.
以 为原点,直线
为原点,直线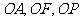 为
为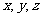 轴建立空间直线坐标系,则有
轴建立空间直线坐标系,则有 ,
,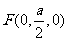 ,
, ,
,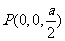 ,
,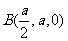 ,
,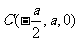 .
.
∵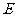 为
为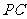 的中点, ∴
的中点, ∴ .
.
(1)易知平面 的法向量为
的法向量为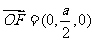 而
而 ,
,
且 , ∴
, ∴ //平面
//平面 .
.
(2)∵ ,
, ∴
∴ ,
,
∴ ,从而
,从而 ,又
,又 ,
,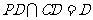 ,
,
∴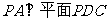 ,而
,而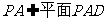 , ∴平面
, ∴平面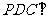 平面
平面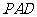
(3)由(2)知平面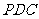 的法向量为
的法向量为 .
.
设平面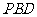 的法向量为
的法向量为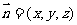 .∵
.∵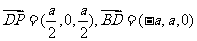 ,
,
∴由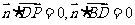 可得
可得 ,令
,令 ,则
,则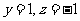 ,
,
故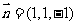 ,∴
,∴ ,
,
即二面角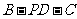 的余弦值为
的余弦值为 ,二面角
,二面角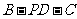 的正切值为
的正切值为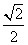 .
.
本题还有其他解法,注意挖掘.
17.(1)设该射手第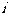 次击中目标的事件为
次击中目标的事件为 ,则
,则 ,…1分
,…1分
该射手恰好射击2次,则第1次没击中目标,第2次击中目标,表示的事件为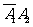 , ……2分
, ……2分
由于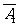 ,
,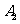 相互独立,则
相互独立,则  .
……4分
.
……4分
即该射手恰好射击两次的概率为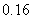 ;
……5分
;
……5分
(2)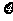 可能取的值为0,1,2,3.
……6分
可能取的值为0,1,2,3.
……6分
由于
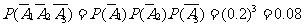 ;
……7分
;
……7分

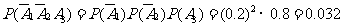 ; ……8分
; ……8分

 ;
……9分
;
……9分
 ;
……10分
;
……10分
则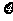 的分布列为
的分布列为
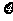 |
0 |
1 |
2 |
3 |
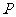 |
0.008 |
0.032 |
0.16 |
0.8 |
……11分
故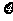 的数学期望为
的数学期望为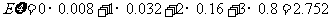 .
……12分
.
……12分
16. (1) 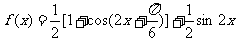 ……2分
……2分
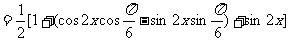
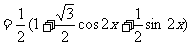 ……4分
……4分
 ,
………5分
,
………5分
∴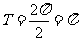 .
. 
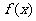 的最小正周期为
的最小正周期为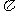 ……6分
……6分
(2)由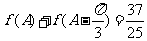 ,得
,得
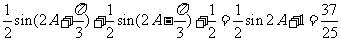 ,则
,则 ,
……8分
,
……8分
∴ ……9分
……9分
由于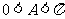 ,则
,则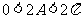 ,
,
但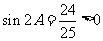 ,则
,则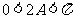 ,即A为锐角,从而
,即A为锐角,从而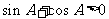 ,
……11分
,
……11分
因此
, .
……12分
.
……12分
(二)选做题(13-15题,考生只能从中选做两题)
13. .解析:由已知有圆的标准方程为
.解析:由已知有圆的标准方程为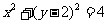 ,设
,设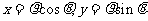 代人方程得
代人方程得 .
.
14.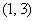 .(注:第14题用集合、不等式表示均可.)解析:
.(注:第14题用集合、不等式表示均可.)解析: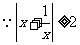 对一切
对一切 且
且 成立,所以
成立,所以 <
<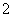 ,
,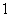 <
<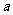 <
< .
.
15. .解析:连接AC,∠DAC=∠DCF=
.解析:连接AC,∠DAC=∠DCF= ,∠BAC=∠BCE=(180-46)/2=
,∠BAC=∠BCE=(180-46)/2=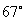 ,所以∠A=∠DAC+∠BAC=
,所以∠A=∠DAC+∠BAC=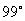 .
.
(一)必做题(9-12题)
9.800,20% (第一空2分,第二空3分).解析:组距为10,则及格的频率为(0.025+0.035+0.01+0.01)×10=0.8,则及格的人数为0.8×1000=800,优秀率=(0.01+0.01)×10×100%=20%.
10. 2.解析:因为 a·b = | a |·| b |·cosq,所以| a×b |2+| a·b|2= | a |2·| b |2,而u = (2,0),u-v = (1,),则v = (1,-),u+v = (3,-),由| u×(u + v) |2+| u·(u + v) |2=| u |2·|(u + v) |2,得| u×(u + v) |2+22=22·(32+3),即| u×(u + v) | =2.
11. .解析:由已知得
.解析:由已知得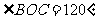 ,OC=15,OB=25,由余弦定理有
,OC=15,OB=25,由余弦定理有 =35,时间
=35,时间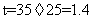 .
.
12.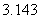 .解析:
.解析: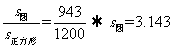 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com