2．直线和平面所成角的定义：　　　　　

　线面角的范围：　　　　　　　　　　　　

[精典范例]

例1：.如图，已知AC，AB分别是平面α的垂线和斜线，C，B分别是垂足和斜足，a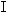α，求证：a⊥BC

例2.求证: 如果平面内的一条直线与这个平面的一条斜线垂直, 那么这条直线就和这条直线在这个平面内的射影垂直.

已知：

求证：

证明：

点评：

上述两题是三垂线定理及其逆定理，今后在证明其它问题时可直接使用。

例3.如图, ∠BAC在平面α内, 点Pα, ∠PAB=∠PAC . 求证: 点P在平面α上的射影在∠BAC的平分线上.

思考：你能设计一个四个面都是直角的四面体吗?

思维点拨：

要证线面垂直，通常是从线线垂直来证明，而要证明线面垂直，通常又是从线线垂直来证明，即线线垂直和线面垂直互相转化．

追踪训练

1.　　 斜线的定义:　　　　　　　　　　　　

斜足定义:　　　　　　　　　　　　

斜线段定义:　　　　　　　　　　　　

2.能熟练地运用直线和平面垂直的判定定理和性质定理.

自学评价

知识网络

		直线和平面所成角的定义

学习要求

1.了解直线和平面所成角的概念和范围;

3.在△ABC中，∠B＝90°，SA⊥面ABC，AM⊥SC，AN⊥SB垂足分别为N、M，

求证：AN⊥BC，MN⊥SC

2.某空间图形的三视图如图所示，试画出它的直观图，并指出其中的线面垂直关系．

1.已知直线l,m,n与平面α，指出下列命题是否正确，并说明理由：

(1)若l⊥α,则l与α相交；

(2)若m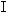α,n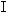α,l⊥m,l⊥n,则l⊥α；

(3)若l//m,m⊥α,n⊥α,则l//m

1、如图, 已知PA⊥α, PB⊥β, 垂足分别为A、B, 且α∩β= l , 求证: AB⊥l .

例2.已知直线l // 平面α , 求证: 直线l各点到平面α的距离相等.

例3.已知正方体ABCD-A₁B₁C₁D₁ .

(1)求证: A₁C⊥B₁D₁ ;

(2)若M、N分别为B₁D₁与C₁D上的点, 且MN⊥B₁D₁ , MN⊥C₁D , 求证: MN//A₁C .

点评：要证线线平行均可利用线面垂直的性质。

追踪训练2

6．直线和平面的距离：

[精典范例]

例1：.求证: 如果两条平行直线中的一条垂直于一个平面, 那么另一条直线也垂直于这个平面.

思维点拔：

要证线面垂直，只要证明直线与平面内的两条相交直线垂直，或利用定义进行证明。

Rt△ABC所在平面外一点S，且SA=SB=SC

(1)求证：点S在斜边中点D的连线SD⊥面ABC

(2)若直角边BA=BC，求证：BD⊥面SAC

追踪训练1

5．直线和平面垂直的性质定理：

已知：

求证：

证明：