1.　　 两个平面的位置关系

位置关系　　两平面平行　两平面相交

公共点

符号表示

图形表示

3.掌握两个平面平行的判定定理和性质定理, 并能运用其解决一些具体问题.

[课堂互动]

自学评价

2.会画平行或相交平面的空间图形, 并会用符号表示.

知识网络

学习要求

1.理解并掌握两平面平行, 两平面相交的定义.

4.在正方体ABCD-A₁B₁C₁D₁中，P为DD₁的中点，O为底面ABCD的中心，

求证：B₁O⊥平面PAC

点拨：使B₁O垂直与平面ABC内的两条相交直线．

[选修延伸]

Rt△ABC的斜边BC在平面M内，两直角边和平面M所成的角分别是45°和30°，求斜边的高AD和平面M所成的角

答：AD和平面M所成的角60°

总结：要求斜线AD与平面M所成的角，找出斜线AD在平面M内的射影是关键．

解题步骤：①作，②证，③求。

追踪训练

在正方体ABCD-A₁B₁C₁D₁中，

①　　　 求AD₁与平面ABCD所成的角，

②　　 求AD₁与平面A₁D₁CB所成的角

(1) 45°

(2) 30°

3.从平面外一点向平面引斜线段，如果斜线段长相等，那么它们在平面内的射影相等吗？

答：相等

2.若直线a与平面α不垂直，那么在平面内α与直线a垂直的直线 (B　 )

A.只有一条　

B.有无数条

C.是平面α内的所有直线

D.不存在

1.如图，∠BCA=90°，PC⊥面ABC，则在三角形ABC，三角形PAC的边所在的直线中：

(1)与PC垂直的直线有AC,AB,BC

(2)与AP垂直的直线有BC　

2．直线和平面所成角的定义：　　　　　

　线面角的范围：　　　　　　　　　　　　

[精典范例]

例1：.如图，已知AC，AB分别是平面α的垂线和斜线，C，B分别是垂足和斜足，aα，求证：a⊥BC

证明：见书36例3

例2.求证: 如果平面内的一条直线与这个平面的一条斜线垂直, 那么这条直线就和这条直线在这个平面内的射影垂直.

已知：

求证：

证明：

证明：略

点评：

上述两题是三垂线定理及其逆定理，今后在证明其它问题时可直接使用。

例3.如图, ∠BAC在平面α内, 点Pα, ∠PAB=∠PAC . 求证: 点P在平面α上的射影在∠BAC的平分线上.

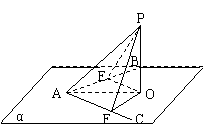
证明：见书36例4

思考：你能设计一个四个面都是直角的四面体吗?

思维点拨：

要证线面垂直，通常是从线线垂直来证明，而要证明线面垂直，通常又是从线线垂直来证明，即线线垂直和线面垂直互相转化．

追踪训练

1.　　 斜线的定义:　　　　　　　　　　　　

斜足定义:　　　　　　　　　　　　

斜线段定义: