
1. 圆柱侧面积公式:见书中(以下同).
2.会求一些简单旋转体的表面积.
[课堂互动]
自学评价
 知识网络
知识网络
学习要求
1. 理解圆柱圆锥圆台的侧面积公式的推导。
5. 一个正六棱台的两个底面的边长分别等于8cm和18cm
, 侧棱长等于13cm , 求它的侧面积.
一个正六棱台的两个底面的边长分别等于8cm和18cm
, 侧棱长等于13cm , 求它的侧面积.
略解:
侧面积=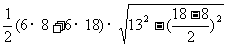
=936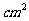
|
学生质疑 |
|
|
教师释疑 |
|
4.一个正三棱锥的侧面都是直角三角形, 底面边长为a , 求它的表面积.
略解:
侧面积=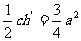 ,底面积=
,底面积=
所以表面积为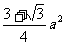 .
.
3.已知正四棱柱的底面边长为3,侧面的对角线长为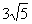 ,则这个正四棱柱的侧面积为 72 .
,则这个正四棱柱的侧面积为 72 .
2.如图,E,F分别为正方形ABCD的边BC,CD的中点,沿图中虚线折起来,它能围成怎样的几何体?
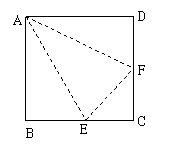
答案:三棱锥(其中有一条侧棱垂直于底面).
1.下列图形中,不是正方体的展开图的是 ( C )


A B


C D
9.三个公式之间的关系:
[精典范例]
例1:一个正六棱柱的侧面都是正方形,底面边长为a,求它的表面积.
[解]
侧面积=
底面积=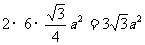
所以表面积为 .
.
例2:设计一个正四棱锥形冷水塔塔顶, 高是0.85m , 底面的边长是1.5m , 制造这种塔顶需要多少平方米铁板? (保留两位有效数字)
[解]
见书中.
思维点拨
记清记准各种侧面积公式,然后结合几何体性质解题.
追踪训练
8.正棱台侧面积公式:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com