3.空间两直线的位置关系(3种关系)：

2.平面的基本性质(3个公理与3个推论) ：

.

1.空间几何体(柱锥台球,三视图) 的概念：

2. 会证线线、线面、面面的平行与垂直的问题,会求简单的线线、线面、面面间的角与距离以及简单几何体的面积与体积的问题.

[课堂互动]

自学评价

知识网络

学习要求

1.温故本章内容，使知识系统化，条理化．分清重点，明确难点，再现注意点，达到巩固与知新的效果。

3．多面体至少有几个面？这个多面体是怎样的几何体。

答：4个面，四面体．

2.右图中的几何体是不是棱台？为什么？ 　

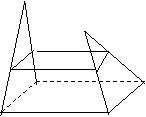
答：不是，因为四条侧棱延长不交于一点．

1. 如图，四棱柱的六个面都是平行四边形。这个四棱柱可以由哪个平面图形按怎样的方向平移得到？

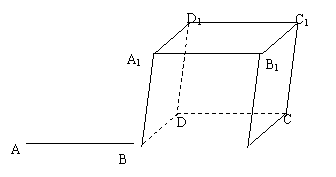
答由四边形ABCD沿AA1方向平移得到．

5．多面体的分类：

⑴棱柱的分类　　　　　　　　　　　　　

⑵棱锥的分类　　　　　　　　　　　　　

⑶棱台的分类　　　　　　　　　　　　　

[精典范例]

例1：设有三个命题：

甲：有两个面平行，其余各面都是平行四边形所围体一定是棱柱；

乙：有一个面是四边形，其余各面都三角形所围成的几何体是棱锥；

丙：用一个平行与棱锥底面的平面去截棱锥，得到的几何体叫棱台。

　以上各命题中，真命题的个数是　　 (A)

A．0　 B. 1　 C. 2　 D. 3

例2：画一个四棱柱和一个三棱台。

[解]四棱柱的作法：

⑴画上四棱柱的底面----画一个四边形；

⑵画侧棱-----从四边形的每一个顶点画平行且相等的线段；

⑶画下底面------顺次连结这些线段的另一个端点

见书7页例1

⑷画一个三棱锥，在它的一条侧棱上取一点，从这点开始，顺次在各个侧面画出与底面平行的线段，将多余的线段檫去．

见书7页例1

点评：(1)被遮挡的线要画成虚线(2)画台由锥截得

思维点拔：

解柱、锥、台概念性问题和画图需要：

(1).准确地理解柱、锥、台的定义

(2).灵活理解柱、锥、台的特点：

例如：棱锥的特点是：⑴两个底面是全等的多边形；⑵多边形的对应边互相平行；⑶棱柱的侧面都是平行四边形。反过来，若一个几何体，具有上面三条，能构成棱柱吗？或者说，上面三条能作为棱柱的定义吗？

答：不能．

点评:就棱柱来验证这三条性质，无一例外，能不能找到反例，是上面三条能作为棱柱的定义的关键。

追踪训练一

4．多面体的定义：