6.如图, 已知AB是平面α的垂线, AC是平面α的斜线, CDα, CD⊥AC, 则面面垂直的有_____________ .

5.在直角三角形ABC中，两直角边AC=b,BC=a,CD⊥AB于D，把三角形ABC沿CD折成直二面角A-CD-B，

求cos ∠ACB＝　　　　 ．

4.等边三角形ABC的边长为1，BC边上的高是AD，若沿高AD将它折成直二面角B－AD－C，则A到BC的距离是　　．

3.已知钝二面角α- l –β等于θ, 异面直线a、b满足aα, bβ, 且a⊥l , b⊥l , 则a , b 所成的角等于　　　 (　　 )

　 A. θB. π－θC.－θD. θ或π－θ

2.过正方形ABCD的顶点A作线段PA垂直于平面ABCD , 如果PA=AB , 那么平面ABP与平面CDP所成的锐二面角为　　 (　　 )

　 A. 30°　 B. 45°C. 60°D. 90°

1.已知二面角α- l –β为锐角，点M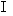α，M到β的距离MN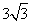＝，M到棱的距离MP＝6，则N点α的距离是　(　　 )

A. 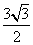　　B. 3　 C. 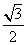　　D.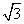

8.如图, 在三棱柱ABC-A₁B₁C₁中, 点E、D分别是B₁C₁与BC的中点. 求证: 平面A₁EB//平面ADC₁

拓展延伸

求证：一条直线和两个平行平面相交，这条直线和这两个平面所成的角相等。

已知：

求证：

证明：

7.已知平面α//β, lβ, 且l//α, 求证: l//β.

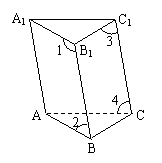
6.如图, 在多面体ABC-A₁B₁C₁中, 如果在平面AB₁内 , ∠1+∠2=180°, 在平面BC₁内 , ∠3+∠4=180°, 那么平面ABC与平面A₁B₁C₁的关系____________ .

5.平面外的一条直线上有两点到这个平面的距离相等, 则直线与该平面的位置关系_____